
【题目】已知□ABCD中,直线m绕点A旋转,直线m不经过B、C、D点,过B、C、D分别作BE⊥m于E, CF⊥m于F, DG⊥m于G.
(1)当直线m旋转到如图1位置时,线段BE、CF、DG之间的数量关系是 _;
(2)当直线m旋转到如图2位置时,线段BE、CF、DG之间的数量关系是 _;
(3)当直线m旋转到如图3的位置时,线段BE、CF、DG之间有怎样的数量关系?请直接写出你的猜想,并加以证明.

【答案】见解析
【解析】解:
(1)如图1,过C作CM⊥DG,交DG的延长线于点M,
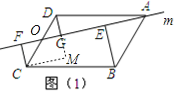
∵DM⊥CM,CF⊥AF,CM⊥DG,
∴∠DMC=∠CFG=∠AEB=90°,
∴四边形GFCM为矩形,
∴FG∥CM,FC=GM,
∵四边形ABCD为平行四边形,
∴CD=AB,CD∥AB,
∴∠DOG=∠BAE=∠DCM,
在△CDM和△ABE中
![]()
∴△CDM≌△ABE(AAS),
∴DM=BE,
∴BE=DG+GM=CF+DG,
故答案为:BE=CF+DG;
(2)如图2,过D作DN⊥CF,交CF于点N,延长CD交AF于点P,
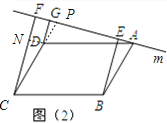
∵DG⊥AF,CF⊥AF,
∴四边形DGFN为矩形,
∴ND∥AF,且DG=NF,
∵四边形ABCD为平行四边形,
∴AB=CD,且AB∥CD,
∴∠CDN=∠DPG=∠BAE,
在△CDN和△BAE中
![]()
∴△CDN≌△BAE(AAS),
∴CN=BE,
∴CF=CN+DF=BE+DG,
故答案为:CF=BE+DG;
(3)猜想:DG=BE+CF;
证明:如图3,过C作CH⊥DG于H,
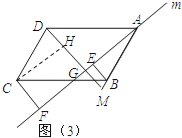
又∵CF⊥m,DG⊥m,
∴四边形CFGH是矩形,
∴CF=HG,
∵DG⊥m,BE⊥m,
∴∠DGE=∠BEG=90°,
∴DG∥BE,
∴∠ABE=∠AMG
∵□ABCD,
∴AD∥BC,CD=AB,
∴∠CDH=∠AMG,
∴∠CDH=∠ABE,
在△CDH和△ABE中
![]()
∴△CDH≌△ABE(AAS),
∴DH=BE,
∴DG=DH+HG=BE+CF,
∴DG=BE+CF.


 智慧小复习系列答案
智慧小复习系列答案科目:初中数学 来源: 题型:
【题目】如图,互相垂直的两条射线OE与OF的端点O在三角板的内部,与三角板两条直角边的交点分别为点D、B.
(1)填空:若∠ABO=50°,则∠ADO= ;
(2)若DC、BP分别是∠ADO、∠ABF的角平分线,如图1.求证:DC⊥BP;
(3)若DC、BP分别分别是∠ADE、∠ABF的角平分线,如图2.猜想DC与BP的位置关系,并说明理由.
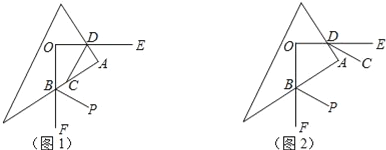
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点A的坐标为(1,2),把点A向右平移2个单位,再向下平移1个单位后得到A’,则点A’的坐标为( )
A. (0,4)B. (3,1)C. (﹣1,3)D. (2,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
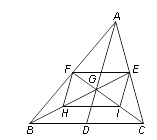
【题目】如图,△ABC的中线AD、BE、CF相交于点G,H、I分别是BG、CG的中点.
(1)求证:四边形EFHI是平行四边形;
(2)①当AD与BC满足条件 时,四边形EFHI是矩形;
②当AD与BC满足条件 时,四边形EFHI是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图所示,在ΔABC和ΔADE中,AB=AC,AD=AE,∠BAC=∠DAE,,且点B,A,D在同一条直线上,连接BE,CD,M,N分别为BE,CD的中点, 连接AM,AN,MN.
⑴.求证:BE=CD
⑵.求证:ΔAMN是等腰三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学活动课上,张老师说:“![]() 是无理数,无理数就是无限不循环小数,同学们,你能把
是无理数,无理数就是无限不循环小数,同学们,你能把![]() 的小数部分全部写出来吗?”大家议论纷纷,晶晶同学说:“要把它的小数部分全部写出来是非常难的,但我们可以用(
的小数部分全部写出来吗?”大家议论纷纷,晶晶同学说:“要把它的小数部分全部写出来是非常难的,但我们可以用(![]() ﹣1)表示它的小数部分.接着,张老师出示了一道练习题:
﹣1)表示它的小数部分.接着,张老师出示了一道练习题:
“已知8+![]() =x+y,其中x是一个整数,且0<y<1,请你求出2x+(
=x+y,其中x是一个整数,且0<y<1,请你求出2x+(![]() ﹣y)2016的值”.请聪明的你给出正确答案.
﹣y)2016的值”.请聪明的你给出正确答案.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com