
【题目】已知,如图,△ABC是等边三角形,AE=CD,BQ⊥AD于Q,BE交AD于点P,
(1)求∠BPQ的度数.
(2)求证:BP=2PQ.

【答案】见解析
【解析】试题分析:
(1)由△ABC是等边三角形可得:AB=AC,∠BAE=∠ACD=60°,结合已知AE=CD,易证△BAE≌△ACD,从而可得∠ABE=∠CAD;由三角形外角的性质易得:∠BPQ=∠BAP+∠ABE,再由∠BAP+∠CAE=∠BAC=60°,可得∠BPQ=∠BAP+∠ABE=∠BAP+∠CAE=60°;
(2)由BQ⊥AD于Q可得∠BQP=90°,结合∠BPQ=60°可得∠PBQ=30°,由直角三角形中30°的锐角所对直角边是斜边的一半可得:PQ=![]() BP,∴BP=2PQ.
BP,∴BP=2PQ.
试题解析:
(1)∵△ABC是等边三角形,
∴AB=AC,∠BAE=∠C=60°,
在△ABE和△CAD中,
∵AB=AC,∠BAE=∠C=60°,AE=CD,
∴△ABE≌△CAD(SAS),
∴∠ABE=∠CAD,
∴∠BPQ=∠BAP+∠ABE=∠BAP+∠CAD=60°.
(2)∵BQ⊥AD,
∴∠BQP=90°,
∴∠PBQ=90°﹣∠BPQ=90°﹣60°=30°,
∴BP=2PQ.


科目:初中数学 来源: 题型:
【题目】某市为了了解高峰时段16路公交车从总站乘该路车出行的人数情况,随机抽查了10个班次乘该路车的人数,结果如下:
14,23,16,25,23,28,26,27,23,25.
(1)这组数据的众数为________,中位数为________;
(2)计算这10个班次乘该路车人数的平均数;
(3)如果16路公交车在高峰时段从总站共出车60个班次,根据上面的计算结果,估计在高峰时段从总站乘该路车出行的乘客共有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,线段CD在线段AB上,且CD=2,若线段AB的长度是一个正整数,则图中以A,B,C,D这四点中任意两点为端点的所有线段长度之和可能是( ) ![]()
A.28
B.29
C.30
D.31
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A,B两点的坐标是A(5,a),B(b,4),若AB平行于x轴,且AB=3,则a+b的值为( )
A. ﹣1 B. 9 C. 12 D. 6或12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂计划生产A,B两种产品共10件,其生产成本和利润如下表:
(1)若工厂计划获利14万元,问A,B两种产品应分别生产多少件?
(2)若工厂计划投入资金不多于44万元,且获利多于14万元,问工厂有哪几种生产方案?
(3)在(2)的条件下,哪种生产方案获利最大?并求出最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下面推理过程:
如图,已知DE∥BC,DF、BE分别平分∠ADE、∠ABC,可推得∠FDE=∠DEB的理由:
∵DE∥BC(已知)
∴∠ADE= .( )
∵DF、BE分别平分∠ADE、∠ABC,
∴∠ADF=![]()
∠ABE=![]() .( )
.( )
∴∠ADF=∠ABE
∴DF∥ .()
∴∠FDE=∠DEB.( )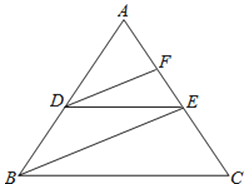
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com