
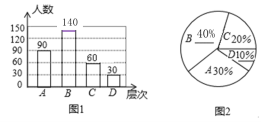
【题目】(10分)居民区内的“广场舞”引起媒体关注,小王想了解本小区居民对“广场舞”的看法,进行了一次抽样调查,把居民对“广场舞”的看法分为四个层次:A.非常赞同;B.赞同但要有时间限制;C.无所谓;D.不赞同.并将调查结果绘制了图1和图2两幅不完整的统计图.
请你根据图中提供的信息解答下列问题:

(1)求本次被抽查的居民有多少人?
(2)将图1和图2补充完整;
(3)求图2中“C”层次所在扇形的圆心角的度数;
(4)估计该小区4000名居民中对“广场舞”的看法表示赞同(包括A层次和B层次)的大约有多少人.
【答案】(1)、300人;(2)、答案见解析;(3)、72°;(4)、2800人.
【解析】
试题分析:(1)、根据A的人数和百分比得出总人数;(2)、根据总人数以及百分比分别求出D和B所占的百分比以及B和C的人数,然后将图形补全;(3)、利用360°乘上C所占的百分比,从而得出圆心角的度数;(4)、首先求出A和B在样本中所占的百分比,然后得出答案.
试题解析:(1)、∵90÷30%=300(人), ∴本次被抽查的居民有300人.
(2)、∵D所占的百分比:30÷300=10%, B所占的百分比:1﹣20%﹣30%﹣10%=40%,
B对应的人数:300×40%=120(人), C对应的人数:300×20%=60(人),
∴补全统计图,如图所示:
(3)、∵360°×20%=72°, ∴“C”层次所在扇形的圆心角的度数为72°.
(4)、∵4000×(30%+40%)=2800(人),
∴估计该小区4000名居民中对“广场舞”的看法表示赞同(包括A层次和B层次)的大约有2800人.


 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() (
(![]() )与y轴交于点A,与x轴交于B,C两点(点C在x轴正半轴上),△ABC为等腰直角三角形,且面积为4,现将抛物线沿BA方向平移,平移后的抛物线过点C时,与x轴的另一点为E,其顶点为F,对称轴与x轴的交点为H.
)与y轴交于点A,与x轴交于B,C两点(点C在x轴正半轴上),△ABC为等腰直角三角形,且面积为4,现将抛物线沿BA方向平移,平移后的抛物线过点C时,与x轴的另一点为E,其顶点为F,对称轴与x轴的交点为H.
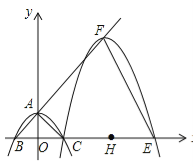
(1)求a、c的值及抛物线的解析式.
(2)连接OF,试判断△OEF是否为等腰三角形,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有4cm和6cm的两根小棒,请你再找一根小棒,并以这三根小棒为边围成一个三角形,下列长度的小棒可选的是( )
A. 1cm B. 2cm C. 7cm D. 10cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题为假命题的个数有( )
①相等的角是对顶角;
②依次连结四边形四边中点所组成的图形是平行四边形;
③在同圆或等圆中,相等的弦所对的圆周角相等;
④在同圆中,平分弦的直径垂直于这条弦.
A. 0个 B. 1个 C. 2个 D. 3个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知坐标平面内的三个点A(1,3),B(3,1),O(0,0),把△ABO向下平移3个单位再向右平2个单位后得△DEF.

(1)直接写出A、B、O三个对应点D、E、F的坐标;
(2)求△DEF的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com