
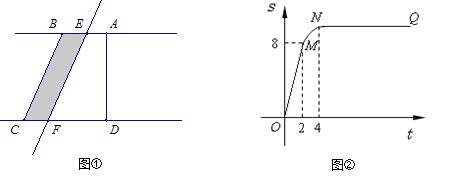
【题目】如图①所示,在直角梯形ABCD中,∠BAD=90°,E是直线AB上一点,过E作直线![]() //BC,交直线CD于点F.将直线
//BC,交直线CD于点F.将直线![]() 向右平移,设平移距离BE为
向右平移,设平移距离BE为![]() (t
(t![]() 0),直角梯形ABCD被直线
0),直角梯形ABCD被直线![]() 扫过的面积(图中阴影部份)为S,S关于
扫过的面积(图中阴影部份)为S,S关于![]() 的函数图象如图②所示,OM为线段,MN为抛物线的一部分,NQ为射线,N点横坐标为4.
的函数图象如图②所示,OM为线段,MN为抛物线的一部分,NQ为射线,N点横坐标为4.
信息读取
(1)梯形上底的长AB= ;(2) 直角梯形ABCD的面积= ;
图象理解
(3)写出图②中射线NQ表示的实际意义;(4) 当![]() 时,求S关于
时,求S关于![]() 的函数关系式;
的函数关系式;
问题解决
(5)当t为何值时,直线l将直角梯形ABCD分成的两部分面积之比为1: 3.
【答案】(1)、2;(2)、12;(3)、当平移距离BE大于等于4时,直角梯形ABCD被直线![]() 扫过的面积恒为12;(4)、S=-
扫过的面积恒为12;(4)、S=-![]() +8t-4;(5)、
+8t-4;(5)、![]() 或
或![]()
【解析】
试题分析:(1)、当点E到达点A时,面积成一次函数,则AB=2;(2)、根图示得出梯形的面积;(3)、根据函数图形得出实际意义;(4)、首先根题意画出图形,然后利用直角梯形的面积减去直角三角形DOF的面积得出函数解析式;(5)、分成0<t<2和2<t<4两种情况分别进行计算.
试题解析:(1)、![]() .
.
(2)、S梯形ABCD=12 .
(3)、当平移距离BE大于等于4时,直角梯形ABCD被直线![]() 扫过的面积恒为12.
扫过的面积恒为12.
(4)、当![]() 时,如下图所示,
时,如下图所示,
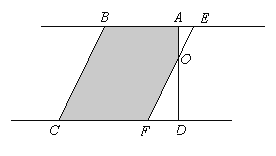
直角梯形ABCD被直线![]() 扫过的面积S=S直角梯形ABCD-SRt△DOF
扫过的面积S=S直角梯形ABCD-SRt△DOF![]() .
.
(5)、①当![]() 时,有
时,有![]() ,解得
,解得![]() .
.
②当![]() 时,有
时,有
![]() ,
,
即![]() ,解得
,解得![]() ,
,![]() (舍去).
(舍去).
答:当![]() 或
或![]() 时,直线l将直角梯形ABCD分成的两部分面积之比为1: 3.
时,直线l将直角梯形ABCD分成的两部分面积之比为1: 3.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,DE⊥AB于E,DF⊥AC于F,若BD=CD,∠ABD与∠C互补.
(1)求证:AD平分∠BAC;(2)若AB=5,AC=9,则AE=_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某家电生产企业根据市场调查分析,决定调整产品生产方案,准备每周(按120个工时计算)生产空调、冰箱、彩电共360台,且彩电至少生产60台,已知生产这些家电产品每台所需工时和每台产值如下表:
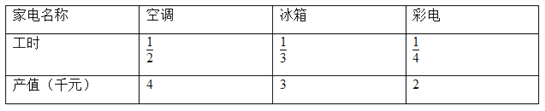
问每周应生产空调、冰箱、彩电各多少台,才能使产值最高?最高产值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一个多项式与3x2+9x的和等于5x2+4x﹣1,则这个多项式是( )
A. 2x2﹣5x﹣1 B. ﹣2x2+5x+1 C. 8x2﹣5x+1 D. 8x2+13x﹣1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某教研机构为了解在校初中生阅读数学教科书的现状,随机抽取某校部分初中学生进行了调查.依据相关数据绘制成以下不完整的统计图表,请根据图表中的信息解答下列问题:


(1)求样本容量及表格中a,b,c的值,并补全统计图;
(2)若该校共有初中生2 300名,请估计该校“不重视阅读数学教科书”的初中生人数;
(3)①根据上面的统计结果,谈谈你对该校初中生阅读数学教科书的现状的看法及建议;
②如果要了解全省初中生阅读数学教科书的情况,你认为应该如何进行抽样?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com