
【题目】如图,在正方形ABCD纸片上有一点P,PA=1,PD=2,PC=3,现将△PCD剪下,并将它拼到如图所示位置(C与A重合,P与G重合,D与D重合),则∠APD的度数为( )
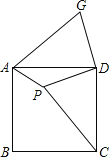
A.150°B.135°C.120°D.108°
【答案】B
【解析】
连接PG,由题意得出PD=GD=2,∠CDP=∠ADG,得出∠PDG=∠ADC=90°,得出△PDG是等腰直角三角形,由等腰直角三角形的性质得出∠GPD=45°,PG=![]() PD=2
PD=2![]() ,得出AP2+PG2=AG2,由勾股定理的逆定理得出∠GPA=90°,即可得出答案.
,得出AP2+PG2=AG2,由勾股定理的逆定理得出∠GPA=90°,即可得出答案.
解:连接PG,如图所示:
∵四边形ABCD是正方形,
∴AD=CD,∠ADC=90°,AG=PC=3,
∵PA=1,PD=2,PC=3,将△PCD剪下,并将它拼到如图所示位置(C与A重合,P与G重合,D与D重合),
∴PD=GD=2,∠CDP=∠ADG,
∴∠PDG=∠ADC=90°,
∴△PDG是等腰直角三角形,
∴∠GPD=45°,PG=![]() PD=2
PD=2![]() ,
,
∵AG=PC=3,AP=1,PG=2![]() ,
,
∴AP2+PG2=AG2,
∴∠GPA=90°,
∴∠APD=90°+45°=135°;
故选:B.


科目:初中数学 来源: 题型:
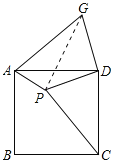
【题目】在矩形中ABCD,AB=12,P是边AB上一点,把△PBC沿直线PC折叠,顶点B的对位点G,过点B作BE⊥CG,垂足为E且在AD上,BE交PC于点F
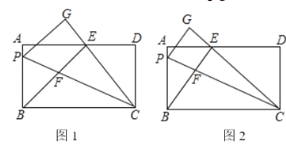
(1)如图1,若点E是AD的中点,求证:△AEB≌△DEC;
(2)如图2,①求证:BP=BF;②当AD=25,且AE<DE时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(给出定义)
若四边形的一条对角线能将四边形分割成两个相似的直角三角形,那么我们将这种四边形叫做“跳跃四边形”,这条对角线叫做“跳跃线”.
(理解概念)
(1)命题“凡是矩形都是跳跃四边形”是什么命题(“真”或“假”).
(2)四边形ABCD为“跳跃四边形”,且对角线AC为“跳跃线”,其中AC⊥CB,∠B=30°,AB=4![]() ,求四边形ABCD的周长.
,求四边形ABCD的周长.
(实际应用)已知抛物线y=ax2+m(a≠0)与x轴交于B(﹣2,0),C两点,与直线y=2x+b交于A,B两点.
(3)直接写出C点坐标,并求出抛物线的解析式.
(4)在线段AB上有一个点P,在射线BC上有一个点Q,P,Q两点分别以![]() 个单位/秒,5个单位/秒的速度同时从B出发,沿BA,BC方向运动,设运动时间为t,当其中一个点停止运动时,另一个点也随之停止运动.在第一象限的抛物线上是否存在点M,使得四边形BQMP是以PQ为“跳跃线”的“跳跃四边形”,若存在,请直接写出t的值;若不存在,请说明理由.
个单位/秒,5个单位/秒的速度同时从B出发,沿BA,BC方向运动,设运动时间为t,当其中一个点停止运动时,另一个点也随之停止运动.在第一象限的抛物线上是否存在点M,使得四边形BQMP是以PQ为“跳跃线”的“跳跃四边形”,若存在,请直接写出t的值;若不存在,请说明理由.
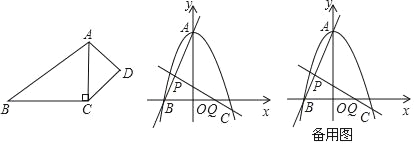
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图①是一个长为![]() 、宽为
、宽为![]() 的长方形,沿图中虚线用剪刀均分成四块小长方形,然后按图②的形状拼成一个正方形.
的长方形,沿图中虚线用剪刀均分成四块小长方形,然后按图②的形状拼成一个正方形.
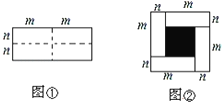
(1)请用两种不同的方法求图②中阴影部分的面积.
方法1: ;
方法2: ;
(2)观察图②请你写出下列三个代数式:![]() 之间的等量关系.
之间的等量关系.
(3)根据(2)题中的等量关系,解决如下问题:
①已知:![]() ,求
,求![]() 的值;
的值;
②已知:![]() ,求:
,求:![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点D,E分别在AB,AC上,DE∥BC,F是AD上一点,FE的延长线交BC的延长线于点G.求证:
(1)∠EGH>∠ADE;
(2)∠EGH=∠ADE+∠A+∠AEF.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A1,A2,A3…都在x轴上,点B1,B2,B3…都在直线y=x上,OA1=1,且△B1A1A2,△B2A2A3,△B3A3A4,…△Bn A n A n+1…分别是以A1,A2,A3,…An…为直角顶点的等腰直角三角形,则△B10A10A11的面积是________.
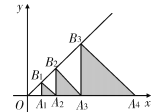
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若一个三角形一条边的平方等于另两条边的乘积,我们把这个三角形叫做比例三角形.

![]() 已知
已知![]() 是比例三角形,
是比例三角形,![]() ,
,![]() ,请直接写出所有满足条件的AC的长;
,请直接写出所有满足条件的AC的长;
![]() 如图1,在四边形ABCD中,
如图1,在四边形ABCD中,![]() ,对角线BD平分
,对角线BD平分![]() ,
,![]() 求证:
求证:![]() 是比例三角形.
是比例三角形.
![]() 如图2,在
如图2,在![]() 的条件下,当
的条件下,当![]() 时,求
时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠ABC=75°,E为BC延长线上一点,∠ABC与∠ACE的平分线相交于点D.则∠D的度数为( )

A.15°B.17.5°C.20°D.22.5°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,△ABC是等边三角形,AE=CD,BQ⊥AD于Q,BE交AD于点P,下列说法:①∠APE=∠C,②AQ=BQ,③BP=2PQ,④AE+BD=AB,其中正确的个数有( )个。
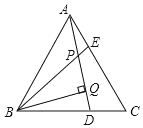
A. 4B. 3C. 2D. 1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com