已知六边形ABCDEF是中心对称图形.AB=1.BC=2.CD=3.那么EF= . 题目和参考答案——青夏教育精英家教网—

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

科目：初中数学 来源： 题型：

（1）已知△ABC为正三角形，点M是射线BC上任意一点，点N是射线CA上任意一点，且BM=CN，直线BN与AM相交于Q点．就下面给出的三种情况（如图①、②、③），先用量角器分别测量∠BQM的大小，然后猜测∠BQM等于多少度，并利用图③证明你的结论．

（2）将（1）中的“正△ABC”分别改为正方形ABCD（如图④）、正五边形ABCDE（如图⑤）．正六边形ABCDEF（如图③）、…、正n边形ABCD…X（如图（n）），“点N是射线CA上任意一点”改为点N是射线CD上任意一点，其余条件不变，根据（1）的求解思路，分别推断∠BQM各等于多少度，将结论填入下表：

查看答案和解析>>

科目：初中数学 来源： 题型：

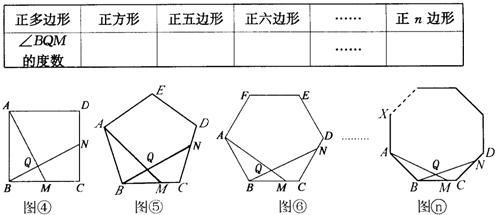
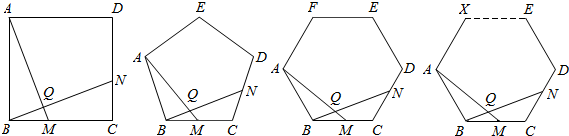
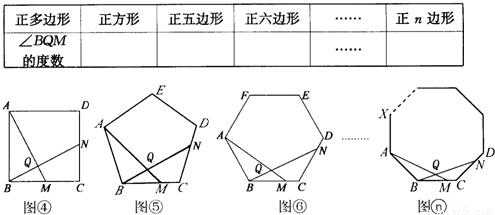
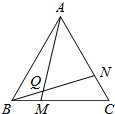（1）已知△ABC为正三角形，点M是BC上一点，点N是AC上一点，AM、BN相交于点Q，∠BAM=∠NBC，猜想∠BQM等于多少度，并证明你的猜想．
（2）将（1）中的“正△ABC”分别改为正方形ABCD、正五边形ABCDE、正六边形ABCDEF、正n边形ABCD…X，“点N是AC上一点”改为点N是CD上一点，其余条件不变，分别推断出∠BQM等于多少度，将结论填入下表：

正多边形	正方形	正五边形	正六边形	…	正n边形
∠BQM的度数				…

查看答案和解析>>

科目：初中数学 来源：2013年山东省青岛市中考数学模拟试卷（七）（解析版） 题型：解答题

（1）已知△ABC为正三角形，点M是射线BC上任意一点，点N是射线CA上任意一点，且BM=CN，直线BN与AM相交于Q点．就下面给出的三种情况（如图①、②、③），先用量角器分别测量∠BQM的大小，然后猜测∠BQM等于多少度，并利用图③证明你的结论．

（2）将（1）中的“正△ABC”分别改为正方形ABCD（如图④）、正五边形ABCDE（如图⑤）．正六边形ABCDEF（如图③）、…、正n边形ABCD…X（如图（n）），“点N是射线CA上任意一点”改为点N是射线CD上任意一点，其余条件不变，根据（1）的求解思路，分别推断∠BQM各等于多少度，将结论填入下表：

查看答案和解析>>

科目：初中数学 来源：2012年山东省济宁市曲阜市中考数学调研试卷（5月份）（解析版） 题型：解答题

（1）已知△ABC为正三角形，点M是射线BC上任意一点，点N是射线CA上任意一点，且BM=CN，直线BN与AM相交于Q点．就下面给出的三种情况（如图①、②、③），先用量角器分别测量∠BQM的大小，然后猜测∠BQM等于多少度，并利用图③证明你的结论．

（2）将（1）中的“正△ABC”分别改为正方形ABCD（如图④）、正五边形ABCDE（如图⑤）．正六边形ABCDEF（如图③）、…、正n边形ABCD…X（如图（n）），“点N是射线CA上任意一点”改为点N是射线CD上任意一点，其余条件不变，根据（1）的求解思路，分别推断∠BQM各等于多少度，将结论填入下表：

查看答案和解析>>

科目：初中数学 来源：2003年山东省泰安市中考数学试卷（解析版） 题型：解答题

（2003•泰安）（1）已知△ABC为正三角形，点M是射线BC上任意一点，点N是射线CA上任意一点，且BM=CN，直线BN与AM相交于Q点．就下面给出的三种情况（如图①、②、③），先用量角器分别测量∠BQM的大小，然后猜测∠BQM等于多少度，并利用图③证明你的结论．

（2）将（1）中的“正△ABC”分别改为正方形ABCD（如图④）、正五边形ABCDE（如图⑤）．正六边形ABCDEF（如图③）、…、正n边形ABCD…X（如图（n）），“点N是射线CA上任意一点”改为点N是射线CD上任意一点，其余条件不变，根据（1）的求解思路，分别推断∠BQM各等于多少度，将结论填入下表：

查看答案和解析>>

练习册

高中

初中

小学