
【题目】我们给出如下定义:若一个四边形的两条对角线相等,则称这个四边形为等对角线四边形.请解答下列问题:
(1)写出你所学过的特殊四边形中是等对角线四边形的两种图形的名称;
(2)探究:当等对角线四边形中两条对角线所夹锐角为60°时,这对60°角所对的两边之和与其中一条对角线的大小关系,并证明你的结论.
【答案】(1)梯形、矩形、正方形;(2)答案见解析
【解析】试题分析:(1)等腰梯形、矩形、正方形,任选两个即可;
(2)等对角线四边形中两条对角线所夹锐角为60°时,这对60°角所对的两边之和大于或等于一条对角线的长.分两种情况证明:当BC与CE不在同一条直线上时,60°角所对的两边之和大于其中一条对角线的长;当BC与CE在同一条直线上时60°角所对的两边之和等于其中一条对角线的长.
试题解析:解:(1)梯形、矩形、正方形;
(2)结论:等对角线四边形中两条对角线所夹锐角为60°时,这对60°角所对的两边之和大于或等于一条对角线的长.
已知:四边形ABCD中,对角线AC,BD交于点O,AC=BD,
且∠AOD=60度.
求证:BC+AD≥AC.
证明:过点D作DF∥AC,在DF上截取DE,使DE=AC.
连接CE,BE.
故∠EDO=60°,四边形ACED是平行四边形.
∵AC=DE,AC=BD,∴DE=BD.
∵∠EDO=60°,∴△BDE是等边三角形,∴DE=BE=AC.
①当BC与CE不在同一条直线上时(如图1),
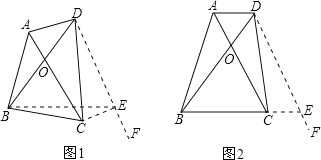
在△BCE中,有BC+CE>BE,∴BC+AD>AC.
②当BC与CE在同一条直线上时(如图2),
则BC+CE=BE.
因此BC+AD=AC
综合①、②,得BC+AD≥AC.
即等对角线四边形中两条对角线所夹角为60°时,这对60°角所对的两边之和大于或等于其中一条对角线的长.


科目:初中数学 来源: 题型:
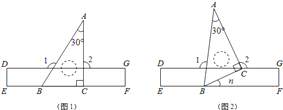
【题目】如图1,把一块含30°的直角三角板ABC的BC边放置于长方形直尺DEFG的EF边上.
(1)填空:∠1= °,∠2= °;
(2)现把三角板绕B点逆时针旋转n°.
①如图2,当0<n<90,且点C恰好落在DG边上时,求∠1、∠2的度数(结果用含n的代数式表示);
②当0<n<360时,是否会存在三角板某一边所在的直线与直尺(有四条边)某一边所在的直线垂直?如果存在,直接写出所有n的值和对应的那两条垂线;如果不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
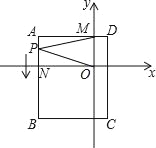
【题目】如图,平面直角坐标系中,ABCD为长方形,其中点A、C坐标分别为(﹣4,2)、(1,﹣4),且AD∥x轴,交y轴于M点,AB交x轴于N.
(1)求B、D两点坐标和长方形ABCD的面积;
(2)一动点P从A出发(不与A点重合),以![]() 个单位/秒的速度沿AB向B点运动,在P点运动过程中,连接MP、OP,请直接写出∠AMP、∠MPO、∠PON之间的数量关系;
个单位/秒的速度沿AB向B点运动,在P点运动过程中,连接MP、OP,请直接写出∠AMP、∠MPO、∠PON之间的数量关系;
(3)是否存在某一时刻t,使三角形AMP的面积等于长方形面积的![]() ?若存在,求t的值并求此时点P的坐标;若不存在请说明理由.
?若存在,求t的值并求此时点P的坐标;若不存在请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在直角坐标系中,O是坐标原点,点A在y轴正半轴上,二次函数y=ax2+ ![]() x+c的图象F交x轴于B、C两点,交y轴于M点,其中B(﹣3,0),M(0,﹣1).已知AM=BC.
x+c的图象F交x轴于B、C两点,交y轴于M点,其中B(﹣3,0),M(0,﹣1).已知AM=BC.
(1)求二次函数的解析式;
(2)证明:在抛物线F上存在点D,使A、B、C、D四点连接而成的四边形恰好是平行四边形,并请求出直线BD的解析式;
(3)在(2)的条件下,设直线l过D且分别交直线BA、BC于不同的P、Q两点,AC、BD相交于N.
①若直线l⊥BD,如图1,试求 ![]() 的值;
的值;
②若l为满足条件的任意直线.如图2.①中的结论还成立吗?若成立,证明你的猜想;若不成立,请举出反例.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.相等的角是对顶角
B.在同一平面内,不平行的两条直线一定互相垂直
C.点P(2,﹣3)在第四象限
D.一个数的算术平方根一定是正数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,点D、E分别在边AC、BC上(不与点A、B、C重合),点P是直线AB上的任意一点(不与点A、B重合).设∠PDA=x,∠PEB=y,∠DPE=m,∠C=n.
(1)如图,当点P在线段AB上运动,且n=90°时
①若PD∥BC,PE∥AC,则m=_____;
②若m=50°,求x+y的值.
(2)当点P在直线AB上运动时,直接写出x、y、m、n之间的数量关系.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,两个大小一样的直角三角形重叠在一起,将其中一个三角形沿着点B到点C的方向平移到![]() 的位置,AB=12cm,DH=4cm,平移的距离是8cm,则阴影面积是________.
的位置,AB=12cm,DH=4cm,平移的距离是8cm,则阴影面积是________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小国同学的父亲参加旅游团到某地旅游,准备买某种礼物送给小国.据了解,沿旅游线路依次有A、B、C三个地点可以买到此种礼物,其质量相当,价格各不相同,但不知哪家更便宜.由于时间关系,随团旅游车不会掉头行驶.
(1)若到A处就购买,写出买到最低价格礼物的概率;
(2)小国同学的父亲认为,如果到A处不买,到B处发现比A处便宜就马上购买,否则到C处购买,这样更有希望买到最低价格的礼物.这个想法是否正确?试通过树状图分析说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
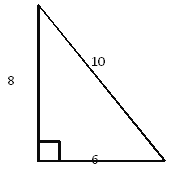
【题目】如图,已知一个边长分别为6、8、10的直角三角形,请设计出一个有一条边长为8的直角三角形,使这两个直角三角形能够拼成一个等腰三角形.
(1)画出4种不同拼法(周长不等)的等腰三角形;
(2)分别求出4种不同拼法的等腰三角形的周长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com