
【题目】如图,在矩形ABCD中,E、F分别是边AB、CD上的点,AE=CF,连接EF、BF,EF与对角线AC交于点O,且BE=BF,∠BEF=2∠BAC.
(1)求证:OE=OF;
(2)求∠ACB的度数.

【答案】(1)证明见解析(2)60°
【解析】(1)根据矩形的对边平行可得AB∥CD,再根据两直线平行,内错角相等求出∠BAC=∠FCO,然后利用“角角边”证明△AOE和△COF全等,再根据全等三角形的即可得证;
(2)连接OB,根据等腰三角形三线合一的性质可得BO⊥EF,再根据矩形的性质可得OA=OB,根据等边对等角的性质可得∠BAC=∠ABO,再根据三角形的内角和定理列式求出∠ABO=30°,即∠BAC=30°,继而求得答案.
(1)∵四边形ABCD是矩形,
∴AB∥CD,
∴∠OCF=∠OAE,
在△OCF和△OAE中,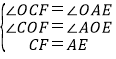
∴△COF≌△AOE(AAS),
∴OE=OF;
(2)如图,连接OB,
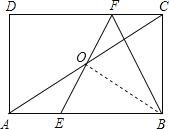
∵BE=BF,OE=OF,
∴BO⊥EF,
∴在Rt△BEO中,∠BEF+∠ABO=90°,
由直角三角形斜边上的中线等于斜边上的一半可知:OA=OB=OC,
∴∠BAC=∠ABO,
又∵∠BEF=2∠BAC,
即2∠BAC+∠BAC=90°,
解得∠BAC=∠ABO=30°,
∴∠ACB=90°-∠BAC=60°.


 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:
【题目】解方程:
(1)x2﹣2x﹣8=0;
(2)3x(x﹣1)=2(x﹣1);
(3)x2+3=3(x+1);
(4)2x(4x+5)=7;
(5)4x2﹣8x+1=0;
(6)(y+2)2=(3y﹣1)2 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O上有两点A与P,且OA⊥OP,若A点固定不动,P点在圆上匀速运动一周,那么弦AP的长度d与时间t的函数关系的图象可能是( )

A.①
B.③
C.①或③
D.②或④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在数轴上点A表示数a,点B表示数b,且a,b满足![]() .
.
(1)点A表示的数为________,点B表示的数为________;
(2)设点A与点C之间的距离表示为AC,点B与点C之间的距离表示为BC.若在数轴上存在一点C,使BC=2AC,则点C表示的数为__________;
(3)若在原点处放一挡板,一小球甲从点A处以每秒2个单位长度的速度向左运动;同时另一小球乙从点B以每秒2个单位长度的速度也向左运动,在碰到挡板后(忽略球的大小,可看做一点)以原来速度的两倍向相反的方向运动.设运动的时间为t秒,请用含t的代数式分别表示出甲、乙两小球到原点的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若两个二次函数图象的顶点、开口方向都相同,则称这两个二次函数为“同簇二次函数”.
(1)请写出两个为“同簇二次函数”的函数;
(2)已知关于x的二次函数y1=2x2﹣4mx+2m2+1和y2=ax2+bx+5,其中y1的图象经过点A(1,1),若y1+y2与y1为“同簇二次函数”,求函数y2的表达式,并求出当0≤x≤3时,y2的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O的直径AB=4,∠ABC=30°,BC交⊙O于D,D是BC的中点. 
(1)求BC的长;
(2)过点D作DE⊥AC,垂足为E,求证:直线DE是⊙O的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,点F为弦AC的中点,连接OF并延长交⊙O于点D,过点D作⊙O的切线,交BA的延长线于点E. 
(1)求证:AC∥DE;
(2)若OA=AE=4,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某射击队教练为了了解队员训练情况,从队员中选取甲、乙两名队员进行射击测试,相同条件下各射靶5次,成绩统计如下:

(1)根据上述信息可知:甲命中环数的中位数是 环,乙命中环数的众数是 环;
(2)试通过计算说明甲、乙两人的成绩谁比较稳定?
(3)如果乙再射击1次,命中8环,那么乙射击成绩的方差会 .(填 “变大”、“变小” 或 “不变”)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数y=kx+b的图象经过点A(0,2)和点B(-a,3),且点B在正比例函数y=-3x的图象上.
(1)求a的值;
(2)求一次函数的解析式并画出它的图象;
(3)若P(m,y1),Q(m-1,y2)是这个一次函数图象上的两点,试比较y1与y2的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com