
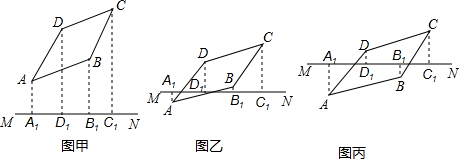
分析 (1)连接AC,BD相交于点O,作OO1⊥MN于点O1,根据梯形中位线定理即可得出结论;
(2)连接AC,BD交于点O,过点O作OG⊥MN,垂足为G,延长OG交AC1的连线于点H,可证明CC1-AA1=BB1+DD1;
(3)连接AC,BD交于点O,连接DB1,AC1,过点O作OG⊥MN,G为垂足,延长OG交DB1于点K,交AC1于点H,利用三角形中位线定理可证明CC1-AA1=DD1-BB1.
解答 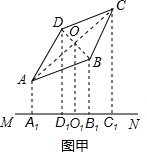 (1)证明:如图甲,连接AC,BD相交于点O,作OO1⊥MN于点O1,
(1)证明:如图甲,连接AC,BD相交于点O,作OO1⊥MN于点O1,
∵AA1⊥MN,CC1⊥MN,
∴AA1∥CC1,
∵O是AC的中点,
∴AA1+CCl=2OO1,
同理,BB1+DDl=2OO1,
∴AA1+CCl=BB1+DDl;
(2)如图乙,连接AC,BD交于点O,过点O作OG⊥MN,垂足为G,延长OG交AC1的连线于点H,
∵四边形ABCD是平行四边形,
∴O是线段AC的中点也是线段BD的中点.
∵CC1⊥MN,
∴OH是△ACC1的中位线,
∴OH=OG+GH=$\frac{1}{2}$CC1.
同理,GH=$\frac{1}{2}$AA1,
∴OG=$\frac{1}{2}$(CC1-AA1),即2OG=CC1-AA1.
∵DD1⊥MN,BB1⊥MN,
∴DD1∥BB1,
∴OG是梯形DD1∥B1B的中位线,
∴DD1∥BB1=2OG,
∴CC1-AA1=BB1+DD1;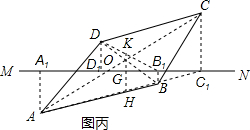
(3)如图丙,连接AC,BD交于点O,连接DB1,AC1,过点O作OG⊥MN,G为垂足,延长OG交DB1于点K,交AC1于点H,
∵CC1⊥MN,O是AC的中点,OH⊥MN,
∴OH是△ACC1的中位线,
∴OH=OG+GH=$\frac{1}{2}$CC1.
同理,GH=$\frac{1}{2}$AA1,OK=$\frac{1}{2}$BB1,GK=OG+OK=$\frac{1}{2}$DD1,
∴OG=$\frac{1}{2}$CC1-GH=$\frac{1}{2}$CC1-$\frac{1}{2}$AA1,即2OG=CC1-AA1.
同理,2OG=DD1-BB1,
∴CC1-AA1=DD1-BB1.
点评 本题考查的是四边形综合题,此题比较复杂,解答此题的关键是作出辅助线,利用平行四边形对角线互相平分的性质构造出梯形及三角形,利用梯形及三角形的中位线定理解答.


科目:初中数学 来源: 题型:选择题
| A. | -a是负数 | |
| B. | 两个相似图形是位似图形 | |
| C. | 随机抛掷一枚质地均匀的硬币,落地后正面朝上 | |
| D. | 平移后的图形与原来对应线段相等 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
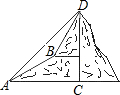 如图,甲乙两数学兴趣小组测量出CD的高度,甲小组在地面A处测量,乙小组在上坡B处测量,AB=200m,甲小组测得山顶D的仰角为45°,山坡B处的仰角为30°;乙小组测得山顶D的仰角为58°,求山CD的高度(结果保留一位小数)
如图,甲乙两数学兴趣小组测量出CD的高度,甲小组在地面A处测量,乙小组在上坡B处测量,AB=200m,甲小组测得山顶D的仰角为45°,山坡B处的仰角为30°;乙小组测得山顶D的仰角为58°,求山CD的高度(结果保留一位小数)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
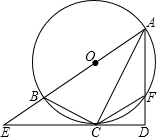 如图,已知AB为⊙O的直径,过⊙O上的点C的切线交AB的延长线于点E,AD⊥EC于点D且交⊙O于点F,连接BC、CF、AC.
如图,已知AB为⊙O的直径,过⊙O上的点C的切线交AB的延长线于点E,AD⊥EC于点D且交⊙O于点F,连接BC、CF、AC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
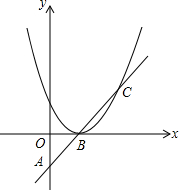 如图,抛物线y=ax2沿着x轴移动,与直线AB相交于B,C两点,若B(1,0)且OA=OB,AB=BC.
如图,抛物线y=ax2沿着x轴移动,与直线AB相交于B,C两点,若B(1,0)且OA=OB,AB=BC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com