
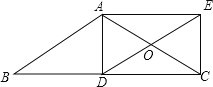
【题目】如图,在△ABC中,AB=AC,点D是边BC的中点,过点A、D分别作BC与AB的平行线,相交于点E,连结EC、AD.
(1)求证:四边形ADCE是矩形;
(2)当∠BAC=90°时,求证:四边形ADCE是正方形.

【答案】(1)、证明过程见解析;(2)、证明过程见解析
【解析】
试题分析:(1)、先由AB=AC,点D是边BC的中点,根据等腰三角形三线合一的性质得出BD=CD,AD⊥BC,再由AE∥BD,DE∥AB,得出四边形AEDB为平行四边形,那么AE=BD=CD,又AE∥DC,根据一组对边平行且相等的四边形是平行四边形得出四边形ADCE是平行四边形,又∠ADC=90°,根据有一个角是直角的平行四边形即可证明四边形ADCE是矩形;(2)、设AC与DE相交于点O.由DE∥AB,根据平行线的性质得出∠DOC=∠BAC=90°,即AC⊥DE,又由(1)知四边形ADCE是矩形,根据对角线互相垂直的矩形是正方形即可证明四边形ADCE是正方形.
试题解析:(1)、∵AB=AC,点D是边BC的中点, ∴BD=CD,AD⊥BC, ∴∠ADC=90°.
∵AE∥BD,DE∥AB, ∴四边形AEDB为平行四边形, ∴AE=BD=CD, 又∵AE∥DC,
∴四边形ADCE是平行四边形, ∵∠ADC=90°, ∴四边形ADCE是矩形;
(2)、设AC与DE相交于点O. ∵DE∥AB,∠BAC=90°, ∴∠DOC=∠BAC=90°, 即AC⊥DE,
又∵由(1)知四边形ADCE是矩形, ∴四边形ADCE是正方形.


科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD中,∠ABC=90°,∠ADC=90°,AB=6,CD=4,BC的延长线与AD的延长线交于点E.
(1)若∠A=60°,求BC的长;
(2)若sinA=![]() ,求AD的长.
,求AD的长.
(注意:本题中的计算过程和结果均保留根号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在某次海上军事学习期间,我军为确保△OBC海域内的安全,特派遣三艘军舰分别在O、B、C处监控△OBC海域,在雷达显示图上,军舰B在军舰O的正东方向80海里处,军舰C在军舰B的正北方向60海里处,三艘军舰上装载有相同的探测雷达,雷达的有效探测范围是半径为r的圆形区域.(只考虑在海平面上的探测)
(1)若三艘军舰要对△OBC海域进行无盲点监控,则雷达的有效探测半径r至少为多少海里?
(2)现有一艘敌舰A从东部接近△OBC海域,在某一时刻军舰B测得A位于北偏东60°方向上,同时军舰C测得A位于南偏东30°方向上,求此时敌舰A离△OBC海域的最短距离为多少海里?
(3)若敌舰A沿最短距离的路线以20![]() 海里/小时的速度靠近△OBC海域,我军军舰B沿北偏东15°的方向行进拦截,问B军舰速度至少为多少才能在此方向上拦截到敌舰A?
海里/小时的速度靠近△OBC海域,我军军舰B沿北偏东15°的方向行进拦截,问B军舰速度至少为多少才能在此方向上拦截到敌舰A?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中正确的是( )
A. 已知a,b,c是三角形的三边,则a2+b2=c2
B. 在直角三角形中,两边的平方和等于第三边的平方
C. 在Rt△ABC中,∠![]() ,所以a2+b2=c2
,所以a2+b2=c2
D. 在Rt△ABC中,∠![]() ,所以a2+b2=c2
,所以a2+b2=c2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com