
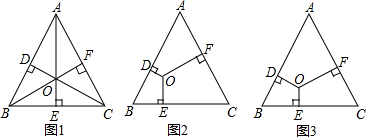
分析 (1)结论1可根据等边三角形的性质,先求出等边△ABC的高为$\sqrt{3}$a,再根据等边三角形三线合一的性质和重心的性质进行求解;结论2根据等边三角形三线合一的性质进行求解;
(2)结论1可通过构建直角三角形,把所求的线段都转化到直角三角形中进行求解;结论2通过构建直角三角形,可根据勾股定理,把所求的线段都表示出来,然后经过化简得出结论是否正确.
解答 解:(1)结论1,结论2成立.
证明:∵点O是等边△ABC的三条高线的交点,
∴AE=BF=CD=$\frac{{\sqrt{3}}}{2}$a,AD=BE=CF=$\frac{1}{2}$a,
∴OD=OE=OF=$\frac{\sqrt{3}}{6}$a,
∴OD+OE+OF=$\frac{{\sqrt{3}}}{2}$a,AD+BE+CF=$\frac{3}{2}$a;
(2)结论1成立.
证明:如图3,过点O作GH∥BC,分别交AB、AC于点G、H,过点H作HM⊥BC于点M,
∴∠DGO=∠B=60°,∠OHF=∠C=60°,
∴△AGH是等边三角形,
∴GH=AH.
∵OE⊥BC,
∴OE∥HM,
∴四边形OEMH是矩形,
∴HM=OE.
在Rt△ODG中,OD=OG•sin∠DGO=OG•sin60°=$\frac{\sqrt{3}}{2}$OG,
在Rt△OFH中,OF=OH•sin∠OHF=OH•sin60°=$\frac{\sqrt{3}}{2}$OH,
在Rt△HMC中,HM=HC•sinC=HC•sin60°=$\frac{\sqrt{3}}{2}$HC,
∴OD+OE+OF=OD+HM+OF=$\frac{\sqrt{3}}{2}$OG+$\frac{\sqrt{3}}{2}$HC+$\frac{\sqrt{3}}{2}$OH
=$\frac{\sqrt{3}}{2}$(GH+HC)=$\frac{\sqrt{3}}{2}$AC=$\frac{\sqrt{3}}{2}$a.
结论2成立.
证明:如图4,连接OA、OB、OC,根据勾股定理得:
BE2+OE2=OB2=BD2+OD2①,
CF2+OF2=OC2=CE2+OE2②,
AD2+OD2=AO2=AF2+OF2③,
①+②+③得:BE2+CF2+AD2=BD2+CE2+AF2,
∴BE2+CF2+AD2=(a-AD)2+(a-BE)2+(a-CF)2=a2-2AD•a+AD2+a2-2BE•a+BE2+a2-2CF•a+CF2
整理得:2a(AD+BE+CF)=3a2
∴AD+BE+CF=$\frac{3}{2}$a.
点评 本题中综合考查了等边三角形的判定和性质,解直角三角形等知识点,由于知识点比较多,本题的难度比较大.


 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
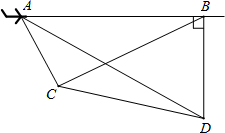 如图,一架飞机以200米/秒的速度由A向B沿水平直线方向飞行,在航线AB的下方有两个山头C、D,飞机在A处时,测得山头C、D在飞机的前方,俯角分别为60°和30°.飞机飞行1分钟后到B处时,往后测得山头C的俯角为30°,而山头D恰好在飞机的正下方.求山头C、D之间的距离.
如图,一架飞机以200米/秒的速度由A向B沿水平直线方向飞行,在航线AB的下方有两个山头C、D,飞机在A处时,测得山头C、D在飞机的前方,俯角分别为60°和30°.飞机飞行1分钟后到B处时,往后测得山头C的俯角为30°,而山头D恰好在飞机的正下方.求山头C、D之间的距离.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com