
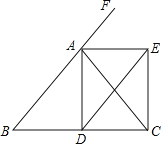
【题目】如图,已知△ABC中,AB=AC,AD是角平分线,F为BA延长线上的一点,AE平分∠FAC,DE∥BA交AE于E.求证:四边形ADCE是矩形.
【答案】见解析
【解析】
首先利用外角性质得出∠B=∠ACB=∠FAE=∠EAC,进而得到AE∥CD,即可求出四边形AEDB是平行四边形,再利用平行四边形的性质求出四边形ADCE是平行四边形,即可求出四边形ADCE是矩形.
证明:∵AB=AC,AD是角平分线,
∴∠B=∠ACB,AD⊥BC,
∵AE平分∠FAC,
∴∠FAE=∠EAC,
∵∠B+∠ACB=∠FAE+∠EAC,
∴∠B=∠ACB=∠FAE=∠EAC,
∴AE∥CD,
又∵DE∥AB,
∴四边形AEDB是平行四边形,
∴AE∥BD,AE=BD,
∵AD⊥BC,AB=AC,
∴BD=DC,
∴AE∥DC,AE=DC,
∴四边形ADCE是平行四边形,
又∵∠ADC=90°,
∴四边形ADCE是矩形.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,已知A(3,0),B(0,-1),连接AB,过B点作AB的垂线段,使BA=BC,连接AC.
(1)如图1,求C点坐标;
(2)如图2,若P点从A点出发,沿x轴向左平移,连接BP,作等腰直角三角形△BPQ,连接CQ.求证:PA=CQ.
(3)在(2)的条件下,若C、P、Q三点共线,求此时P点坐标及∠APB的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
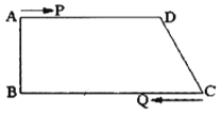
【题目】如图,在四边形ABCD中,AD//BC,![]() ,AD=24 cm,AB=8 cm, BC=26 cm,动点P从A开始沿AD边向D以1cm/s的速度运动;Q从点C开始沿CB边向B以3 cm/s的速度运动.P、Q分别从点A、C同时出发,当其中一点到达端点时,另外一点也随之停止运动.
,AD=24 cm,AB=8 cm, BC=26 cm,动点P从A开始沿AD边向D以1cm/s的速度运动;Q从点C开始沿CB边向B以3 cm/s的速度运动.P、Q分别从点A、C同时出发,当其中一点到达端点时,另外一点也随之停止运动.
(1)当运动时间为t秒时,用含t的代数式表示以下线段的长: AP=________, BQ=__________;
(2)当运动时间为多少秒时,四边形PQCD为平行四边形?
(3)当运动时间为多少秒时,四边形ABQP为矩形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(十九),用四个螺丝将四条不可弯曲的木条围成一个木框,不计螺丝大小,其中相邻两螺丝的距离依序为2、3、4、6,且相邻两木条的夹角均可调整。若调整木条的夹角时不破坏此木框,则任两螺丝的距离之最大值为何?

(A) 5 (B) 6 (C) 7 (D) 10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠BAC的内角平分线与外角平分线分别交BC及BC的延长线于点P、Q.
(1)求∠PAQ的大小;
(2)若点M为PQ的中点,求证:PM2=CM·BM.
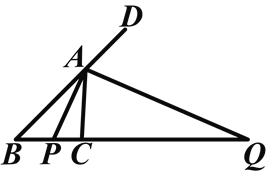
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,垂足为点
,垂足为点![]() ,且
,且![]() ,连接
,连接![]() .
.
(1)如图①,求证:![]() 是等边三角形;
是等边三角形;

(2)如图①,若点![]() 、
、![]() 分别为
分别为![]() ,
,![]() 上的点,且
上的点,且![]() ,求证:
,求证:![]() ;
;
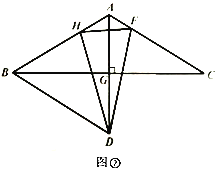
(3)利用(1)(2)中的结论,思考并解答:如图②,![]() 为
为![]() 上一点,连结
上一点,连结![]() ,当
,当![]() 时,线段
时,线段![]() ,
,![]() ,
,![]() 之间有何数量关系,给出证明.
之间有何数量关系,给出证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
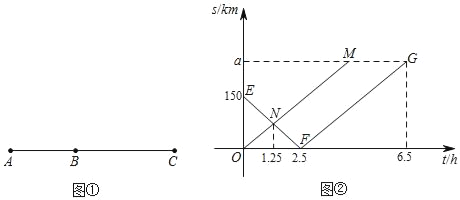
【题目】如图①,A、B、C三地依次在一直线上,两辆汽车甲、乙分别从A、B两地同时出发驶向C地,如图②,是两辆汽车行驶过程中到C地的距离s(km)与行驶时间t(h)的关系图象,其中折线段EF﹣FG是甲车的图象,线段OM是乙车的图象.
(1)图②中,a的值为 ;点M的坐标为 ;
(2)当甲车在乙车与B地的中点位置时,求行驶的时间t的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com