
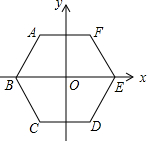
 如图,边长为4的正六边形ABCDEF的中心与坐标原点O重合,AF∥x轴,将正六边形ABCDEF绕原点O顺时针旋转n次,每次旋转60°.当n=2017时,顶点A的坐标为(2,2$\sqrt{3}$).
如图,边长为4的正六边形ABCDEF的中心与坐标原点O重合,AF∥x轴,将正六边形ABCDEF绕原点O顺时针旋转n次,每次旋转60°.当n=2017时,顶点A的坐标为(2,2$\sqrt{3}$). 分析 将正六边形ABCDEF绕原点O顺时针旋转2017次时,点A所在的位置就是原F点所在的位置.
解答  解:2017×60°÷360°=336…1,即与正六边形ABCDEF绕原点O顺时针旋转1次时点A的坐标是一样的.
解:2017×60°÷360°=336…1,即与正六边形ABCDEF绕原点O顺时针旋转1次时点A的坐标是一样的.
当点A按顺时针旋转60°时,与原F点重合.
连接OF,过点F作FH⊥x轴,垂足为H;
由已知EF=4,∠FOE=60°(正六边形的性质),
∴△OEF是等边三角形,
∴OF=EF=4,
∴F(2,2$\sqrt{3}$),即旋转2017后点A的坐标是(2,2$\sqrt{3}$),
故答案是:(2,2$\sqrt{3}$).
点评 此题主要考查了正六边形的性质,坐标与图形的性质-旋转.此题难度适中,注意掌握辅助线的作法,注意数形结合思想的应用.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:选择题
| A. | 27354 | B. | 40000 | C. | 50000 | D. | 1200 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在平面直角坐标系xOy中,直线y=$\frac{1}{2}$x+b与双曲线y=$\frac{4}{x}$的一个交点为A(m,2),与y轴分别交于点B.
在平面直角坐标系xOy中,直线y=$\frac{1}{2}$x+b与双曲线y=$\frac{4}{x}$的一个交点为A(m,2),与y轴分别交于点B.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com