练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
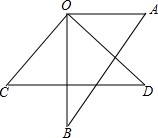
    15．如图，已知∠COD=∠BOA=90°．
    （1）求证：∠AOD=∠BOC；
    （2）求证：∠BOD+∠AOC=180°．

    分析 （1）根据∠COD=∠BOA=90°可得∠COB+∠BOD=∠BOD+∠AOD，即可得证；
    （2）由∠AOC=∠COD+∠AOD知∠BOD+∠AOC=∠BOD+∠COD+∠AOD=∠COD+∠AOB即可得证．

    解答 证明：（1）∵∠COD=∠BOA=90°，
    ∴∠COB+∠BOD=∠BOD+∠AOD，
    ∴∠AOD=∠BOC；

    （2）∵∠AOC=∠COD+∠AOD，
    ∴∠BOD+∠AOC=∠BOD+∠COD+∠AOD=∠COD+∠AOB，
    又∵∠COD=∠BOA=90°，
    ∴∠BOD+∠AOC=180°．

    点评 本题主要考查同角的余角相等，熟练掌握补、余角性质：等角的补角相等．等角的余角相等是关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    5．已知弦AB把圆周分成2：3的两部分，则弧$\widehat{AB}$所对圆心角的度数是（　　）
    A．72°B．72°或144°C．144°D．144°或216°

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    6．某路口南北方向信号灯的设置时间为：红灯25s，绿灯30s，黄灯5s．王老师随机地由南往北开车到达该路口，他遇到绿灯的概率是（　　）
    A．$\frac{6}{11}$B．$\frac{5}{12}$C．$\frac{1}{12}$D．$\frac{1}{2}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

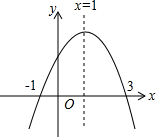    3．如图为二次函数y=ax2+bx+c（a≠0）的图象，则下列说法：①2a+b=0；②a+b+c＞0；③当-1＜x＜3时，y＞0；④-a+c＜0．其中正确的个数为（　　）
    A．1B．2C．3D．4

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    10．解答下列各题：
    （1）x取何值时，代数式3x+2的值不大于代数式4x+3的值？
    （2）当m为何值时，关于x的方程$\frac{1}{2}$x-1=m的解不小于3？
    （3）已知不等式2（x+3）-4＜0，化简：|4x+1|-|2-4x|

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    20．用小立方块搭一个几何体，如图所示，这样的几何体最少需要9个小立方块，最多需要13个小立方块．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    7．下列说法正确的是（　　）
    A．由5m=6m+2可得m=2
    B．方程的解就是方程中未知数所取的值
    C．方程2x-1=3的解是x=2
    D．方程x=-x没有解

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．甲、乙两车分别从相距360km的 A、B两地出发，甲车速度为72km/h，乙车速度为48km/h．
    （1）两车同时出发，相向而行，两车何时相遇？
    （2）两车同时出发，同向而行（乙车在前甲车在后），两车何时相遇？
    （3）两车同时出发，同向而行，多长时间后两车相距120km？

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    5．与-2ab是同类项的为（　　）
    A．-2acB．$\frac{{2{x^2}y}}{3}$C．abD．-2abc

    查看答案和解析>>

    同步练习册答案