
 如图,AB是半圆的直径,AC是一条弦,D是$\widehat{AC}$的中点,DE⊥AB于E,交AC于F,DB交AC于G.求证:
如图,AB是半圆的直径,AC是一条弦,D是$\widehat{AC}$的中点,DE⊥AB于E,交AC于F,DB交AC于G.求证:分析 (1)连接AD,根据同角的余角相等得到∠ADE=∠ABD,根据等弧所对的圆周角相等得到∠DAC=∠ABD,得到答案;
(2)根据对顶角相等证明∠EDB=∠DGF,等量代换得到答案.
解答 证明:(1)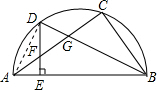 连接AD,
连接AD,
∵AB是半圆的直径,
∴∠ADB=90°,又DE⊥AB,
∴∠ADE=∠ABD,
∵D是$\widehat{AC}$的中点,
∴∠DAC=∠ABD,
∴∠ADE=∠DAC,
∴FA=FD;
(2)∵∠ADE=∠DBC,∠ADE+∠EDB=90°,∠DBC+∠CGB=90°,
∴∠EDB=∠CGB,又∠DGF=∠CGB,
∴∠EDB=∠DGF,
∴FA=FG.
点评 本题考查的是圆周角定理和圆心角、弧、弦之间的关系,掌握直径所对的圆心角是直角、同弧所对的圆周角相等是解题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 直线m的图象如图所示.试求y与x的函数关系式.小华的解法为:设y=kx.由图象可得2=3k.故k=$\frac{2}{3}$.所以y与x的函数关系式为y=$\frac{2}{3}$x,请你评判小华的做法,如果不正确.请给出正确的作法.
直线m的图象如图所示.试求y与x的函数关系式.小华的解法为:设y=kx.由图象可得2=3k.故k=$\frac{2}{3}$.所以y与x的函数关系式为y=$\frac{2}{3}$x,请你评判小华的做法,如果不正确.请给出正确的作法.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,二次函数的图象经过A、B、C三点,点A的坐标为(-1,0),点B的坐标为(4,0),点C在y轴正半轴上,且OB=OC.
如图,二次函数的图象经过A、B、C三点,点A的坐标为(-1,0),点B的坐标为(4,0),点C在y轴正半轴上,且OB=OC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,将边长为$\sqrt{3}$的正方形ABCD绕点A逆时针方向旋转30°后得到正方形AB′C′D′.
如图,将边长为$\sqrt{3}$的正方形ABCD绕点A逆时针方向旋转30°后得到正方形AB′C′D′.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com