
分析 (1)把M(m,4-m)代入y=$\frac{k}{x}$求出k的值,然后把y=3x代入y=$\frac{m(4-m)}{x}$得出方程3x2+m2-4m=0,根据根的判别式求出即可;
(2)根据题意得出3m=4-m或3m=m-4,解方程求得M的坐标,代入解析式即可求得k的值;
(3)①分别代入x=-3和x=-$\frac{1}{2}$,求得等于的函数值,根据函数值和反比例函数的性质求得即可;
②求得交点坐标,根据交点坐标和图象即可求得.
解答 解:(1)把M(m,4-m)代入y=$\frac{k}{x}$得:k=m(4-m),
即这个函数的解析式为y=$\frac{m(4-m)}{x}$;
把y=3x代入y=$\frac{m(4-m)}{x}$得:3x2+m2-4m=0,
△=02-4×3•(m2-4m)=-12m2+48m,
∵y=$\frac{k}{x}$的图象与直线y=3x有交点,
∴-12m2+48m≥0,
即m2-4m≤0,
m(m-4)≤0,
∴0≤m≤4,
即m的取值范围是:0≤m≤4.
(2)∵点M到x轴的距离是到y轴距离的3倍,
∴3m=4-m或3m=m-4,
解得m=1或-2,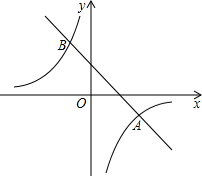
∴M(1,3)或(-2,6),
∴k的值为3或-12;
(3)①∵y=-$\frac{12}{x}$,
当x=-3时,y=-$\frac{12}{-3}$=4,
当x=-$\frac{1}{2}$时,y=-$\frac{12}{-\frac{1}{2}}$=24,
∴当-3<x≤-$\frac{1}{2}$时,求y的取值范围是4<y≤24;
②解$\left\{\begin{array}{l}{y=-x+4}\\{y=-\frac{12}{x}}\end{array}\right.$得$\left\{\begin{array}{l}{{x}_{1}=6}\\{{y}_{2}=-2}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{2}=-2}\\{{y}_{2}=6}\end{array}\right.$,如图,
∴当x≤-2或0<x≤6时,一次函数y=-x+4的值不小于反比例函数y=$\frac{k}{x}$的值.
点评 本题考查了一次函数和反比例函数的交点问题,用待定系数法求反比例函数的解析式,根的判别式以及函数和不等式的关系等知识点的应用,主要考查学生计算能力和理解能力.


 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:初中数学 来源: 题型:解答题
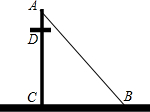 如图,AC为一根电线杆,钢缆AB的长为5m,钢缆底端B与电线底端C的距离为3m,在D处有一个蜘蛛窝.两只蜘蛛同时从点D出发以同样的速度沿路径D-A-B和路径D-C-B织网,结果正好在点B相遇,求蜘蛛窝D的高度.
如图,AC为一根电线杆,钢缆AB的长为5m,钢缆底端B与电线底端C的距离为3m,在D处有一个蜘蛛窝.两只蜘蛛同时从点D出发以同样的速度沿路径D-A-B和路径D-C-B织网,结果正好在点B相遇,求蜘蛛窝D的高度.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
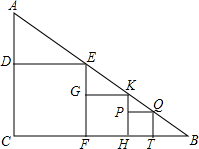 如图,在Rt△ABC中,∠C=90°,AC:BC=1:2,在Rt△ABC中有多个依次排队的正方形DCFE,GFHK,PHTQ…,如果第一个正方形的边长为a,则第2012个正方形的边长应为$\frac{{2}^{2012}}{{3}^{2012}}$.
如图,在Rt△ABC中,∠C=90°,AC:BC=1:2,在Rt△ABC中有多个依次排队的正方形DCFE,GFHK,PHTQ…,如果第一个正方形的边长为a,则第2012个正方形的边长应为$\frac{{2}^{2012}}{{3}^{2012}}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0.3474×1011 | B. | 3.474×1010 | C. | 34.74×109 | D. | 3.474×1011 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com