练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

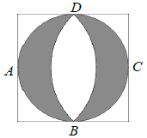
    【题目】文艺复兴时期，意大利艺术大师达芬奇曾研究过圆弧所围成的许多图形的面积问题. 如图所示称为达芬奇的“猫眼”，可看成圆与正方形的各边均相切，切点分别为，所在圆的圆心为点（或）. 若正方形的边长为2，则图中阴影部分的面积为（ ）

    A. B. 2C. D.

    【答案】B

    【解析】

    分别连接AD，AB，BD，构造扇形ABD，等腰直角ABD及弓形，用扇形ABD的面积减去等腰直角ABD的面积，即得到弓形面积，再用圆的面积减去2倍弓形面积即可．

    ∵圆与正方形的各边均相切，切点分别为A，B，C，D，
    ∴A，B，C，D分别是正方形各边中点，
    如图所示，分别连接AD，AB，BD，

    则∠DAB=90°，
    ∵正方形边长为2，
    ∴AD=BD=，
    S扇形ABD-S△ABD=,

    ∴S阴影=S圆.

    故选：B.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图1，E为矩形ABCD边AD上一点，点P从点B沿折线BE﹣ED﹣DC运动到点C时停止，点Q从点B沿BC运动到点C时停止，它们运动的速度都是1cm/s．若P，Q同时开始运动，设运动时间为t（s），△BPQ的面积为y（cm2）．已知y与t的函数图象如图2，则下列结论错误的是【 】

    A．AE=6cm B．

    C．当0＜t≤10时， D．当t=12s时，△PBQ是等腰三角形

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某通讯公司就上宽带网推出A，B，C三种月收费方式．这三种收费方式每月所需的费用y（元与上网时间x(h)的函数关系如图所示，则下列判断错误的是　　

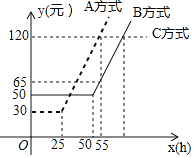
    A. 每月上网时间不足25h时，选择A方式最省钱 B. 每月上网费用为60元时，B方式可上网的时间比A方式多

    C. 每月上网时间为35h时，选择B方式最省钱 D. 每月上网时间超过70h时，选择C方式最省钱

    查看答案和解析>>

    科目：初中数学 来源： 题型：

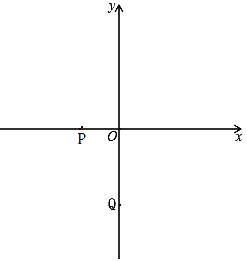
    【题目】如图，已知：P（-1，0），Q（0，-2）.

    （1）求直线PQ的函数解析式；

    （2）如果M（0，）是线段OQ上一动点，抛物线经过点M和点P，

    ①求抛物线与轴另一交点N的坐标（用含，的代数式表示）；

    ②若PN=是，抛物线有最大值+1，求此时的值；

    ③若抛物线与直线PQ始终都有两个公共点，求的取值范围.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】探究：在一次聚会上，规定每两个人见面必须握手，且只握手1次.

    （1）若参加聚会的人数为3，则共握手___次；若参加聚会的人数为5，则共握手___次；

    （2）若参加聚会的人数为（为正整数），则共握手___次；

    （3）若参加聚会的人共握手28次，请求出参加聚会的人数.

    拓展：嘉嘉给琪琪出题：“若线段上共有个点（含端点,），线段总数为30，求的值.”

    琪琪的思考：“在这个问题上，线段总数不可能为30.”琪琪的思考对吗？为什么？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在中，，过点作于点，点是线段上一动点，过三点作交于点，过点作交的延长线于点，交于点.

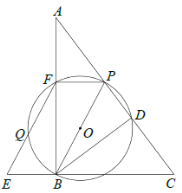
    （1）求证：四边形为平行四边形.

    （2）当时，求的长.

    （3）在点整个运动过程中，

    ①当中满足某两条线段相等，求所有满足条件的的长.

    ②当点三点共线时，交于点，记的面积为，的面积为，求的值. （请直接写出答案）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

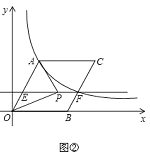
    【题目】如图①，为坐标原点，点在轴的正半轴上，四边形是四边形，，反比例函数在第一象限内的图像经过点，与交于点

    (1)若，求反比例函数解析式；

    (2)若点为的中点，且的面积，求的长和点的坐标；

    (3)在(2)中的条件下，过点作，交于点(如图②)，点为直线上的一个动点，连接，是否存在这样的点，使以为顶点的三角形的直角三角形？若存在，请直接写出所有点的坐标；若不存在，请说明理由.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在□ABCD中，用直尺和圆规作∠BAD的平分线AG交BC于点E．若BF＝6，AB＝5，则AE的长为____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

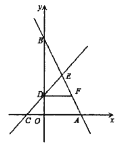
    【题目】如图，直线分别与x轴、y轴交于点和点B，直线分别与x轴、y轴交于点C和点D，两直线交于第一象限内的点E，并且点D为的中点。

    （1）求直线的解析式；

    （2）过点D作轴，交直线于点F，求的面积.

    查看答案和解析>>

    同步练习册答案