
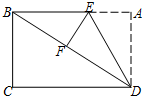
 如图,将矩形纸片ABCD折叠,使边AD落在对角线BD上,折痕为DE,且A点落在对角线F处.若AD=3,CD=4,则AE的长为( )
如图,将矩形纸片ABCD折叠,使边AD落在对角线BD上,折痕为DE,且A点落在对角线F处.若AD=3,CD=4,则AE的长为( )| A. | $\frac{3}{2}$ | B. | 1 | C. | 2 | D. | $\frac{3}{4}$ |
分析 根据矩形对边相等可得AB=CD,再利用勾股定理列式求出BD,根据翻折的性质可得DF=AD,EF=AE,∠DFE=∠A=90°,然后求出BF,设AE=x,表示出BE,在Rt△BEF中,利用勾股定理列方程求解即可.
解答 解:在矩形ABCD中,AB=CD=4,
由勾股定理得,BD=$\sqrt{A{B}^{2}+A{D}^{2}}$=$\sqrt{{4}^{2}+{3}^{2}}$=5,
∵矩形纸片ABCD折叠,边AD落在对角线BD上,A点落在对角线F处
∴DF=AD=3,EF=AE,∠DFE=∠A=90°,
∴BF=BD-DF=5-3=2,
设AE=x,则BE=4-x,
在Rt△BEF中,由勾股定理得,BF2+EF2=BE2,
即22+x2=(4-x)2,
解得x=$\frac{3}{2}$,
即AE的长为$\frac{3}{2}$.
故选A.
点评 本题考查了翻转变换的性质,勾股定理,翻折前后对应线段相等,对应角相等,此类题目,难点在于将所求的线段以及已知线段的长度转化到一个直角三角形中并利用勾股定理列出方程.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
| A. | AB=A′B′,BC=B′C′,∠A=∠A′ | |
| B. | ∠A=∠A′,∠B=∠B′,AC=B′C′ | |
| C. | ∠A=∠A′,∠B=∠B′,∠C=∠C′ | |
| D. | AB=A′B′,BC=B′C′,△ABC的周长等于△A′B′C′的周长 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 自来水销售价格 | 污水处理价格 | |
| 每户每月用水量 | 单价:元/吨 | 单价:元/吨 |
| 17吨及以下 | a | 0.80 |
| 超过17吨不超过30吨的部分 | b | 0.80 |
| 超过30吨的部分 | 6.00 | 0.80 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
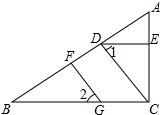 如图,若∠1=∠2,DE∥BC,则:①FG∥DC;②∠AED=∠ACB;③CD平分∠ACB;④∠1+∠B=90°;⑤∠BFG=∠BDC,其中正确的结论是( )
如图,若∠1=∠2,DE∥BC,则:①FG∥DC;②∠AED=∠ACB;③CD平分∠ACB;④∠1+∠B=90°;⑤∠BFG=∠BDC,其中正确的结论是( )| A. | ①②③ | B. | ①②⑤ | C. | ①③④ | D. | ③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
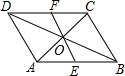 如图,AB∥CD,且AB=CD,AC交DB于点O,过点O的直线EF分别交AB、CD与点E、F,则图中全等的三角形有( )
如图,AB∥CD,且AB=CD,AC交DB于点O,过点O的直线EF分别交AB、CD与点E、F,则图中全等的三角形有( )| A. | 6对 | B. | 5对 | C. | 4对 | D. | 3对 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com