练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】计算下列各题

    （1）（﹣ab）3（5a2b﹣4ab2）；

    （2）（2x﹣1）（4x2+2x+1）

    （3）求5x（2x+1）﹣（2x+3）（5x﹣1）的值，其中x=12．

    【答案】（1）﹣5a5b4+4a4b5（2）8x3﹣1（3）﹣8x+3，﹣93

    【解析】

    （1）原式利用积的乘方运算法则计算，再利用单项式乘以多项式法则计算即可求出值；

    （2）原式利用立方差公式计算即可求出值；

    （3）原式利用单项式乘以多项式，以及多项式乘以多项式法则计算，去括号合并得到最简结果，把x的值代入计算即可求出值．

    （1）原式= =﹣5a5b4+4a4b5；

    （2）原式=8x3﹣1；

    （3）原式=10x2+5x﹣10x2﹣13x+3=﹣8x+3

    当x=12时，原式=﹣96+3=﹣93．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

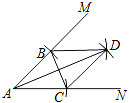
    【题目】如图，以A点为圆心，以相同的长为半径作弧，分别与射线AM，AN交于B，C两点，连接BC，再分别以B，C为圆心，以相同长（大于BC）为半径作弧，两弧相交于点D，连接AD，BD，CD．若∠MBD=40°，则∠NCD的度数为_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】猜想与证明： 如图，摆放矩形纸片ABCD与矩形纸片ECGF，使B、C、G三点在一条直线上，CE在边CD上，连接AF，若M为AF的中点，连接DM，EM．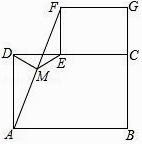

    （1）试猜想写出DM与EM的数量关系，并证明你的结论． 拓展与延伸：
    （2）若将“猜想与证明”中的纸片换成正方形纸片ABCD与正方形纸片ECGF，其他条件不变，则（1）中的结论是否仍然成立？请直接写出你的判断．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

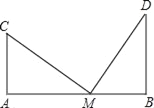
    【题目】如图，两根旗杆AC与BD相距12m，某人从B点沿AB走向A，一定时间后他到达点M，此时他仰望旗杆的顶点C和D，两次视线夹角为90°，且CM=DM．已知旗杆AC的高为3m，该人的运动速度为0、5m/s，求这个人走了多长时间？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

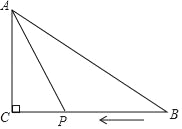
    【题目】如图，在三角形ABC中，∠C＝90°，AC＝6cm，BC＝10cm，点P从B点开始向C点运动速度是每秒1cm，设运动时间是t秒，

    （1）用含t的代数式来表示三角形ACP的面积．

    （2）当三角形ACP的面积是三角形ABC的面积的一半时，求t的值，并指出此时点P在BC上的什么位置？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，△ABC是等腰直角三角形，∠BAC=90°，AB=AC，四边形ADEF是正方形，点B、C分别在边AD、AF上，此时BD=CF，BD⊥CF成立．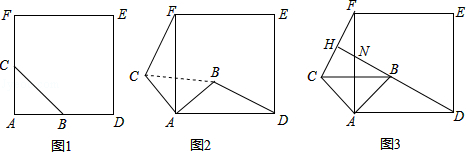

    （1）当△ABC绕点A逆时针旋转θ（0°＜θ＜90°）时，如图2，BD=CF成立吗？若成立，请证明，若不成立，请说明理由；
    （2）当△ABC绕点A逆时针旋转45°时，如图3，延长BD交CF于点H．
    ①求证：BD⊥CF；
    ②当AB=2，AD=3 时，求线段DH的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列说法不正确的有（　　）

    ①一个三角形至少有2个锐角；②在△ABC中，若∠A=2∠B=3∠C，则△ABC为直角三角形；③过n边形的一个顶点可作（n﹣3）条对角线；④n边形每增加一条边，则其内角和增加360°．

    A. 1个 B. 2个 C. 3个 D. 4个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，lA，lB分别表示A步行与B骑车在同一路上行驶的路程S与时间t的关系．

    （1）B出发时与A相距______千米．

    （2）B走了一段路后，自行车发生故障，进行修理，所用的时间是______小时．

    （3）B出发后______小时与A相遇．

    （4）若B的自行车不发生故障，保持出发时的速度前进，______小时与A相遇，相遇点离B的出发点______千米．在图中表示出这个相遇点C．

    （5）求出A行走的路程S与时间t的函数关系式。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为了方便居民低碳出行，聊城市公共自行车租赁系统（一期）试运行．图①是公共自行车的实物图，图②是公共自行车的车架示意图，点A、D、C、E在同一条直线上，CD=30cm，DF=20cm，AF=25cm，FD⊥AE于点D，座杆CE=15cm，且∠EAB=75°．
    （1）求AD的长；
    （2）求点E到AB的距离．（精确到0.1cm，参考数据：sin75°≈0.97，cos75°≈0.26，tan75°≈3.73）

    查看答案和解析>>

    同步练习册答案