
 甲、乙两人同时从相距180千米的A地前往B地,甲乘汽车,乙骑摩托车,甲到达B地停留1小时后返回A地.如图是他们离A地的距离y(千米)与时间x(时)之间的函数关系图象.
甲、乙两人同时从相距180千米的A地前往B地,甲乘汽车,乙骑摩托车,甲到达B地停留1小时后返回A地.如图是他们离A地的距离y(千米)与时间x(时)之间的函数关系图象.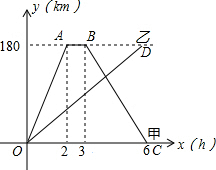
|
|
|
|
|


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
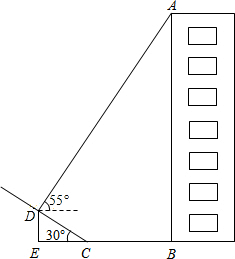 如图,某小区楼房附近有一个斜坡,小张发现楼房在水平地面与斜坡处形成的投影中,在斜坡上的影子长CD=6m,坡角到楼房的距离CB=4m.在D点处观察点A的仰角为55°,已知坡角为30°,你能求出楼房AB的高度吗?(sin55°≈0.82,cos55°≈0.57,tan55°≈1.43,结果精确到0.1m)
如图,某小区楼房附近有一个斜坡,小张发现楼房在水平地面与斜坡处形成的投影中,在斜坡上的影子长CD=6m,坡角到楼房的距离CB=4m.在D点处观察点A的仰角为55°,已知坡角为30°,你能求出楼房AB的高度吗?(sin55°≈0.82,cos55°≈0.57,tan55°≈1.43,结果精确到0.1m)查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com