
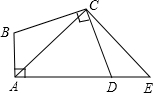
 如图,在四边形ABCD中,∠A=∠BCD=90°,BC=CD.延长AD到E点,使DE=AB.
如图,在四边形ABCD中,∠A=∠BCD=90°,BC=CD.延长AD到E点,使DE=AB.分析 (1)根据等角的补角相等即可证明;
(2)由BC=DC,∠ABC=∠EDC,AB=DE,根据SAS即可证明△CDE≌△CBA.
解答 (1)证明:∵∠A=∠BCD=90°
∴∠ABC+∠ADC=180°,∠ADC+∠CDE=180°,
∴∠ABC=∠EDC,
(2)解:
在△ABC和△EDC中,
$\left\{\begin{array}{l}{BC=DC}\\{∠ABC=∠EDC}\\{AB=DE}\end{array}\right.$
∴△CDE≌△CBA(SAS),
∴AC=CE
点评 本题考查全等三角形的判定和性质、等角的补角相等等知识,解题的关键是正确寻找全等三角形解决问题,属于中考常考题型.


 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:初中数学 来源: 题型:选择题
 如图,在△ABC中,AD⊥BC,BE⊥AC,垂足分别为点D,E,AD与BE交于点F,BF=AC,∠ABE=22°,∠CAD的度数是( )
如图,在△ABC中,AD⊥BC,BE⊥AC,垂足分别为点D,E,AD与BE交于点F,BF=AC,∠ABE=22°,∠CAD的度数是( )| A. | 23° | B. | 22° | C. | 32° | D. | 33° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,高BF、CE相交于点H.
如图,在△ABC中,高BF、CE相交于点H.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图.在矩形ABCD中.AB=6.BC=8.点A在直线1上,AD与直线1相交所得的锐角为60°,点F在直线1上.AF=8.EF⊥直线1.垂足为点F.且EF=6.以EF为直径.在EF的左侧作半圆O.点M是半圆O上任一点.
如图.在矩形ABCD中.AB=6.BC=8.点A在直线1上,AD与直线1相交所得的锐角为60°,点F在直线1上.AF=8.EF⊥直线1.垂足为点F.且EF=6.以EF为直径.在EF的左侧作半圆O.点M是半圆O上任一点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
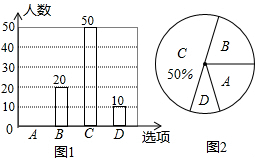 共享单车近日成为市民新宠,越来越多的居民选择共享单车作为出行的交通工具,某中学课外兴趣小组为了了解某小区居民每周使用共享单车时间的情况,随机抽取了该小区部分使用共享单车的居民进行调查(问卷调查表如图所示),并用调查结果绘制了图1、图2两幅每周使用共享单车时间的人数统计图(均不完整),请根据统计图解答以下问题:
共享单车近日成为市民新宠,越来越多的居民选择共享单车作为出行的交通工具,某中学课外兴趣小组为了了解某小区居民每周使用共享单车时间的情况,随机抽取了该小区部分使用共享单车的居民进行调查(问卷调查表如图所示),并用调查结果绘制了图1、图2两幅每周使用共享单车时间的人数统计图(均不完整),请根据统计图解答以下问题:| 选项 | 使用时间t(小时) | |
| A | 0<t≤2 | |
| B | 2<t≤2.5 | |
| C | 2.5<t≤3 | |
| D | t>3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | B. | 2$\sqrt{3}$×3$\sqrt{3}$=6$\sqrt{3}$ | C. | ($\sqrt{3}-\sqrt{2}$)×($\sqrt{3}+\sqrt{2}$)=1 | D. | ($\sqrt{3}+\sqrt{2}$)2=3+2=5 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com