
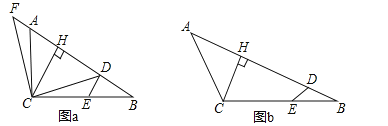
【题目】如图,在△ABC中,BC>AC,点E在BC上,CE=CA,点D在AB上,连接DE,∠ACB+∠ADE=180°,作CH⊥AB,垂足为H.
(1)如图a,当∠ACB=90°时,连接CD,过点C作CF⊥CD交BA的延长线于点F.
①求证:FA=DE;
②请猜想三条线段DE,AD,CH之间的数量关系,直接写出结论;
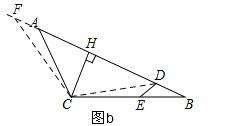
(2)如图b,当∠ACB=120°时,三条线段DE,AD,CH之间存在怎样的数量关系?请证明你的结论.
【答案】(1)①证明见解析;②DE+AD=2CH;(2)AD+DE=![]() CH.
CH.
【解析】
试题分析:(1)①根据ASA证明△AFC≌△EDC,可得结论;
②结论是:DE+AD=2CH,根据CH是等腰直角△FCD斜边上的中线得:FD=2CH,再进行等量代换可得结论;
(2)如图b,根据(1)作辅助线,构建全等三角形,证明△FAC≌△DEC得AF=DE,FC=CD,得等腰△FDC,由三线合一的性质得CH,是底边中线和顶角平分线,得直角△CHD,利用三角函数得出HD与CH的关系,从而得出结论.
试题解析:(1)①∵CF⊥CD,∴∠FCD=90°,∵∠ACB=90°,∴∠FCA+∠ACD=∠ACD+∠DCE,∴∠FCA=∠DCE,∵∠FAC=90°+∠B,∠CED=90°+∠B,∴∠FAC=∠CED,∵AC=CE,∴△AFC≌△EDC,∴FA=DE,②DE+AD=2CH,理由是:
∵△AFC≌△EDC,∴CF=CD,∵CH⊥AB,∴FH=HD,在Rt△FCD中,CH是斜边FD的中线,∴FD=2DH,∴AF+AD=2CH,∴DE+AD=2CH;
(2)AD+DE=![]() CH,理由是:
CH,理由是:
如图b,作∠FCD=∠ACB,交BA延长线于F,∵∠FCA+∠ACD=∠ACD+∠DCB,∴∠FCA=∠DCB,∵∠EDA=60°,∴∠EDB=120°,∵∠FAC=120°+∠B,∠CED=120°+∠B,∴∠FAC=∠CED,∵AC=CE,∴△FAC≌△DEC,∴AF=DE,FC=CD,∵CH⊥FD,∴FH=HD,∠FCH=∠HCD=60°,在Rt△CHD中,tan60°=![]() ,∴DH=
,∴DH=![]() CH,∵AD+DE=AD+AF=FD=2DH=
CH,∵AD+DE=AD+AF=FD=2DH=![]() CH,即:AD+DE=
CH,即:AD+DE=![]() CH.
CH.


科目:初中数学 来源: 题型:
【题目】已知事件A:小明刚到教室,上课铃声就响了:事件B:掷一枚质地均匀的骰子(骰子的六个面上分别刻有1到6的点数),向上一面的点数不大于6.下列说法正确的是( )
A. 只有事件A是随机事件 B. 只有事件B是随机事件
C. 都是随机事件 D. 都是确定性事件
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在梯形ABCD中,AD//BC,E是BC的中点,AD=5,BC=12,CD=![]() ,∠C=45°,点P是BC边上一动点,设PB的长为x。
,∠C=45°,点P是BC边上一动点,设PB的长为x。
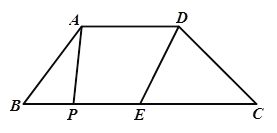
(1)梯形ABCD的面积为_________;
(2)当x的值为___________时,以点P、A、D、E为顶点的四边形为直角梯形;
(3)当x的值为___________时,以点P、A、D、E为顶点的四边形为平行四边形;
(4)点P在BC边上运动的过程中,以P、A、D、E为顶点的四边形能否构成菱形?试说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我县今年4月某地6天的最高气温如下(单位℃):32,29,30,32,30,32.则这个地区最高气温的众数和中位数分别是( )
A.30,32
B.32,30
C.32,31
D.32,32
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com