
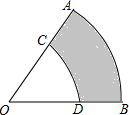
 ��ͼ����֪����OAB������OCD��ͬ��Բ��OA=R��OC=r��
��ͼ����֪����OAB������OCD��ͬ��Բ��OA=R��OC=r������ ��1���������ε������ʽ���㼴�ɣ�
��2����B��OB�Ĵ��߲���ȡBE=OD������OE�Ĵ�ֱƽ���ߣ�OFΪֱ�DZߵĵ���ֱ��������OEF�����ǵõ�OF��Ϊ����
���  �⣺��1���������=S����AOB-S����COD=$\frac{60•�С�{8}^{2}}{360}$-$\frac{60•�С�{6}^{2}}{360}$=$\frac{14��}{3}$��
�⣺��1���������=S����AOB-S����COD=$\frac{60•�С�{8}^{2}}{360}$-$\frac{60•�С�{6}^{2}}{360}$=$\frac{14��}{3}$��
�ʴ�Ϊ��$\frac{14��}{3}$��
��2����ͼ��ʾ��
��������B��BE��OB����ȡBE=OD������OE����OE�Ĵ�ֱƽ���ߣ�����OEΪб�ߵĵ���ֱ��������OEF��OFΪֱ�DZߣ���OF=r�䣮
���� ���⿼�������ε������ʽ��������ͼ��������ε������ʽ�ǽ���Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 5.01��1010 | B�� | 5.01��109 | C�� | 50.1��109 | D�� | 0.501��1010 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -2 | B�� | �� | C�� | 3 | D�� | $\sqrt{6}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
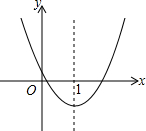 ��ͼ�����κ���y=ax2+bx+c��ͼ����ͼ��ʾ��������˵����ac��0����2a+b��0���۵�x=1ʱ��a+b+c��0���ܵ�x=-1ʱ��a-b+c��0���ݹ���x��һԪ���η���ax2+bx+c=0����������ȵ�ʵ����������Ϊ������ȷ���У�������
��ͼ�����κ���y=ax2+bx+c��ͼ����ͼ��ʾ��������˵����ac��0����2a+b��0���۵�x=1ʱ��a+b+c��0���ܵ�x=-1ʱ��a-b+c��0���ݹ���x��һԪ���η���ax2+bx+c=0����������ȵ�ʵ����������Ϊ������ȷ���У�������| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 4�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
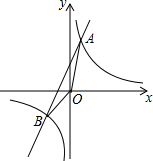 ��֪����������y1=$\frac{k}{x}$��ͼ����һ�κ���y2=ax+b��ͼ���ڵ�A��1��4���͵�B��m��-2����
��֪����������y1=$\frac{k}{x}$��ͼ����һ�κ���y2=ax+b��ͼ���ڵ�A��1��4���͵�B��m��-2�����鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com