
(1)问题探究
数学课上,李老师给出以下命题,要求加以证明.
如图1,在△ABC中,M为BC的中点,且MA= BC,求证∠BAC=90°.
BC,求证∠BAC=90°.
同学们经过思考、讨论、交流,得到以下证明思路:
思路一 直接利用等腰三角形性质和三角形内角和定理…
思路二 延长AM到D使DM=MA,连接DB,DC,利用矩形的知识…
思路三 以BC为直径作圆,利用圆的知识…
思路四…
请选择一种方法写出完整的证明过程;
(2)结论应用
李老师要求同学们很好地理解(1)中命题的条件和结论,并直接运用(1)命题的结论完成以下两道题:
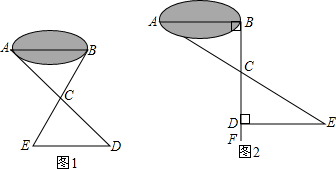
①如图2,线段AB经过圆心O,交⊙O于点A,C,点D在⊙O上,且∠DAB=30°,OA=a,OB=2a,求证:直线BD是⊙O的切线;
②如图3,△ABC中,M为BC的中点,BD⊥AC于D,E在AB边上,且EM=DM,连接DE,CE,如果∠A=60°,请求出△ADE与△ABC面积的比值.

(1)问题研究,证明见解析
(2)①证明见解析
②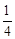 。
。
【解析】
试题分析:(1)应用思路一:根据条件可以得出BM=CM=MA,由等腰三角形的性质就可以得出∠1=∠B,∠2=∠C,由三角形内角和定理就可以求出结论。
(2)①连接OD,CD,由圆的性质就可以得出AO=OD=OC=a,再由条件就可以得出△ODC是等边三角形,由外角与内角的关系就可以求出∠BDC=30°,从而得出∠ODB=90°而得出结论。
②运用(1)的结论可以得出∠ADB=∠ACE=90°,从而有△ADB∽△AEC,由相似的性质可以得出△ADE∽△ABC,由相似三角形的面积之比等于相似比平方,最后由锐角三角形函数值就可以求出结论。
解:(1)问题研究,应用思路一:
∵M为BC的中点,∴BM=CM=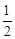 BC。
BC。
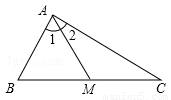
∵MA=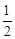 BC,∴BM=CM=MA。
BC,∴BM=CM=MA。
∴∠1=∠B,∠2=∠C。
∵∠1+∠B+∠2+∠C=180°,∴2∠1+2∠2=180°。
∴∠1+∠2=90°,即∠BAC=90°。
(2)①证明:连接OD,CD,
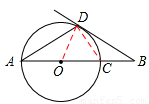
∵∠DAB=30°,OA=a,
∴AO=OD=OC=a,∠BOD=2∠A=60°。
∴△ODC是等边三角形。
∴CD=OC=a,∠DCO=∠CDO=60°。
∵OB=2a,∴BC=a。∴BC=DC。∴∠B=∠BDC。
∴2∠BDC=60°。∴∠BDC=30°。∴∠BDO=∠BDC+∠CDO=90°。
∵OD是⊙O的半径,∴直线BD是⊙O的切线。
②∵M为BC的中点,BD⊥AC于D,∴DM=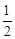 BC。
BC。
∵EM=DM,∴EM=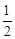 BC。∴∠BEC=90°。∴∠ADB=∠ACE=90°。
BC。∴∠BEC=90°。∴∠ADB=∠ACE=90°。
∵∠A=∠A,∴△ADB∽△AEC。
∴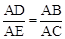 。∴
。∴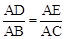 。
。
∵∠A=∠A,∴△ADE∽△ABC。∴ 。
。
∵cos∠A=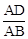 ,且∠A=60°,∴
,且∠A=60°,∴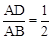 。∴
。∴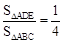 。
。
∴△ADE与△ABC面积的比值为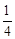 。
。


 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案科目:初中数学 来源: 题型:
| 能力 | 运算 | 数据 处理 |
空间 想象 |
逻辑 思维 |
解决实际问题 | 探究 |
| 分值 | 25 | 15 | 10 | 20 | 20 | 10 |
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 能力 | 运算 | 数据 处理 | 空间 想象 | 逻辑 思维 | 解决实际问题 | 探究 |
| 分值 | 25 | 15 | 10 | 20 | 20 | 10 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com