
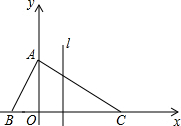
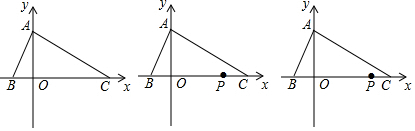
 如图,△ABC的三个顶点坐标分别为(0,2),(-1,0)和(3,0),动点P从原点O出发(点P不与原点O重合),沿x轴的正方向以每秒1个单位长度的速度匀速运动,过点P作直线l⊥x轴,设点P的运动时间为t(秒).
如图,△ABC的三个顶点坐标分别为(0,2),(-1,0)和(3,0),动点P从原点O出发(点P不与原点O重合),沿x轴的正方向以每秒1个单位长度的速度匀速运动,过点P作直线l⊥x轴,设点P的运动时间为t(秒).分析 (1)根据轴对称画出图形即可;
(2)利用轴对称的性质,对应角相等,对应边相等,再用同位角相等,两直线平行即可得出结论;
(3)分两种情况,利用相似三角形的性质和三角形的面积的差即可得出结论
解答 解:(1)①如图1,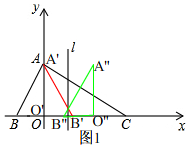 △ABO关于y轴对称的图形为△A′B′O′;
△ABO关于y轴对称的图形为△A′B′O′;
②如图1,△A′B′O′关于直线l对称的图形为△A″B″O″;
(2)A''B''∥AB且A''B''=AB,
理由:∵△ABO关于y轴对称的图形为△A′B′O′;
∴AB=A'B',∠ABO=∠A'B'O',
∵△A′B′O′关于直线l对称的图形为△A″B″O″;
∴A'B'=A''B'',∠A'B'O'=∠A''B''O'',
∴AB=A''B'',∠ABO=∠A''B''O'',
∴AB∥A''B'',
∴A''B''∥AB且A''B''=AB;
(3)当0<t≤$\frac{3}{2}$时,如图2,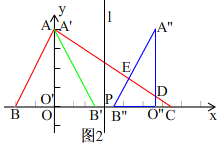 由点B'是点B关于直线l的对称点,
由点B'是点B关于直线l的对称点,
∴B'(1,0),∴OB'=1,
∵△A'O'B'与△A''O''B''关于直线l对称,
∴OB''=OO''-O''B''=2t-1,
∴B''C=OC-OB''=3-(2t-1)=4-2t=2(2-t),
O''C=OC-OB''-O''B''=3-(2t-1)-1=3-2t,
∵tan∠OCA=$\frac{2}{3}$=$\frac{DO''}{CO''}$,
∴DO''=$\frac{2}{3}$CO''=$\frac{2}{3}$(3-2t),
∴S△CDO''=$\frac{1}{2}$CO''×DO''=$\frac{1}{2}$×(3-2t)×$\frac{2}{3}$(3-2t)=$\frac{1}{3}$(3-2t)2,
∴OA=2,BC=4,
∴S△ABC=$\frac{1}{2}$BC×OA=4,
由(2)知,A''B''∥AB,
∴△CB''E∽△CBA,
∴$\frac{{S}_{△B''CE}}{{S}_{△CBA}}=(\frac{B''C}{BC})^{2}$,
∴$\frac{{S}_{△B''CE}}{4}=\frac{4(2-t)^{2}}{16}$,
∴S△B''CE=(2-t)2,
∴S=S△B''CE-S△CDO''=(2-t)2-$\frac{1}{3}$(3-2t)2=$\frac{1}{3}$t2+1
当$\frac{3}{2}$<t≤2时,如图3,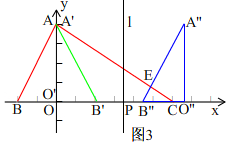 由点B'是点B关于直线l的对称点,
由点B'是点B关于直线l的对称点,
∴B'(1,0),
∴OB'=1,
∵△A'O'B'与△A''O''B''关于直线l对称,
∴OB''=OO''-O''B''=2t-1,
∴B''C=OC-OB''=3-(2t-1)=4-2t=2(2-t),
∵OA=2,BC=4,
∴S△ABC=$\frac{1}{2}$BC×OA=4,
由(2)知,A''B''∥AB,
∴△CB''E∽△CBA,
∴$\frac{{S}_{△B''CE}}{{S}_{△CBA}}=(\frac{B''C}{BC})^{2}$,
∴$\frac{{S}_{△B''CE}}{4}=\frac{4(2-t)^{2}}{16}$,
∴S△B''CE=(2-t)2,
∴S=S△B''CE=(2-t)2,
∴S=$\left\{\begin{array}{l}{\frac{1}{3}{t}^{2}+1(0<t≤\frac{3}{2})}\\{(2-t)^{2}(\frac{3}{2}<t≤2)}\end{array}\right.$.
点评 此题是三角形综合题,主要考查了轴对称的性质,平行线的性质和判定,相似三角形的性质和判定,三角形的面积公式,解本题的关键是利用相似三角形的面积比等于相似比的平方,是一道中等难度的中考常考题.


科目:初中数学 来源: 题型:解答题
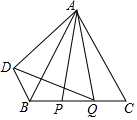 如图,△ABC是等边三角形,AB=2cm,动点P、Q分别从点B、C同时出发,运动速度均为2cm/s.点P从B点出发,沿B→C运动,到点C停止,点Q从点C出发,沿C→B运动,到点B停止,连接AP、AQ,点P关于直线AB的对称点为D,连接BD、DQ,设点P的运动时间为t(s).
如图,△ABC是等边三角形,AB=2cm,动点P、Q分别从点B、C同时出发,运动速度均为2cm/s.点P从B点出发,沿B→C运动,到点C停止,点Q从点C出发,沿C→B运动,到点B停止,连接AP、AQ,点P关于直线AB的对称点为D,连接BD、DQ,设点P的运动时间为t(s).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,抛物线y=ax2+bx与x轴交于点A(4,0),点B(1,3)在抛物线上,点C、B关于抛物线的对称轴对称,过点B作直线BH⊥x轴,交x轴于点H.
如图,抛物线y=ax2+bx与x轴交于点A(4,0),点B(1,3)在抛物线上,点C、B关于抛物线的对称轴对称,过点B作直线BH⊥x轴,交x轴于点H.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com