
【题目】[问题解答]
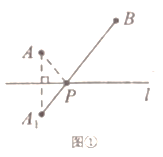
两个城镇![]() 与一条公路
与一条公路![]() 位置如图①所示.现电信部门需在公路
位置如图①所示.现电信部门需在公路![]() 上修建一座信号发射塔
上修建一座信号发射塔![]() 要求发射塔
要求发射塔![]() 到两个城镇
到两个城镇![]() 与
与![]() 的距离之和最短.
的距离之和最短.
解:点![]() 作关于直线
作关于直线![]() 的对称点
的对称点![]() 连结
连结![]() ,
,
与直线![]() 的交点即为所求的点
的交点即为所求的点![]() .
.
![]() 点
点![]() 关于直线
关于直线![]() 对称,
对称,
![]() 直线
直线![]() 垂直平分
垂直平分![]()
![]()
![]()
![]() 点
点![]() 即为所求的点。(两点之间线段最短)
即为所求的点。(两点之间线段最短)
请根据以上问题解答,完成下列问题.
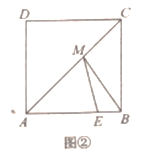
[方法运用]如图②,在正方形![]() 中,
中,![]() 点
点![]() 在边
在边![]() 上,点
上,点![]() 在对角线AC上,
在对角线AC上,
(1)当点![]() 是边
是边![]() 的中点时,则
的中点时,则![]() 的最小值为 ;
的最小值为 ;
(2)若![]() 求
求![]() 周长的最小值.
周长的最小值.
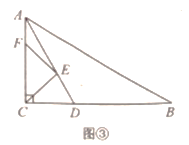
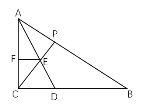
[拓展提升]如图③,在![]() 中,
中,![]() ,AD平分
,AD平分![]() 交
交![]() 于点
于点![]() ,点
,点![]() 分别在
分别在![]() 上,则
上,则![]() 的最小值为 .
的最小值为 .
【答案】[方法运用](1)![]() ;(2)△BEM周长的最小值6;[拓展提升]
;(2)△BEM周长的最小值6;[拓展提升]![]() .
.
【解析】
[方法运用]
(1)易知B关于AC的对称点D,连接DE交AC于M,则![]() 的最小值为DE,根据勾股定理即可求出DE长;
的最小值为DE,根据勾股定理即可求出DE长;
(2)作点E作关于AC的对称点E1,连结BE1,交AC与点M,求出![]() 的最小值,即可求出三角形周长的最小值;
的最小值,即可求出三角形周长的最小值;
[拓展提升]
由角平分线可得到F点对称点始终在AB上,延长CE交AB于P点,则CP=![]() ,当CP⊥AB时,即可求得最小值.
,当CP⊥AB时,即可求得最小值.
解:[方法运用]
(1)易知B点关于AC对称点为D点,连接DE交AC于M,
![]() 的最小值为
的最小值为![]() ,
,
∴则![]() 的最小值为
的最小值为![]() .
.
(2)作点E作关于AC的对称点E1,连结BE1,交AC与点M.
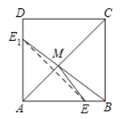
∵点E、E1关于AC对称,
∴AC垂直平分EE1
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
又∵BE=4-3=1,
∴△BEM周长的最小值6.
[拓展提升]
∵AD平分![]() ,
,
∴F点关于AD的对称点始终在AB上,
延长CE交AB于P点,则P点为F点的对称点,即CP=![]() ,
,
∴当CP⊥AB时,有最小值,
∵![]() ,
,
∴AB=5,
∴CP=![]()
∴![]() 的最小值为
的最小值为![]() .
.


 口算题天天练系列答案
口算题天天练系列答案科目:初中数学 来源: 题型:
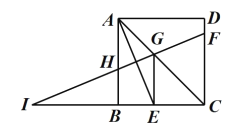
【题目】如图,在正方形![]() 中,
中,![]() 平分
平分![]() ,交
,交![]() 于点
于点![]() 垂直平分线段
垂直平分线段 ![]() ,分别交
,分别交![]() 、
、 ![]() 、
、![]() 延长线于点
延长线于点![]() 、
、![]() 、
、![]() ,则下列结论: ①
,则下列结论: ①![]() ; ②
; ② ![]() ; ③
; ③ ![]() ; ④
; ④ ![]() .其中正确的结论是__________.(填写所有正确结论的序号)
.其中正确的结论是__________.(填写所有正确结论的序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
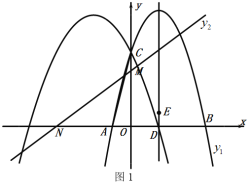
【题目】如图1,抛物线![]() 与抛物线
与抛物线![]() 相交y轴于点C,抛物线
相交y轴于点C,抛物线![]() 与x轴交于A、B两点(点B在点A的右侧),直线
与x轴交于A、B两点(点B在点A的右侧),直线![]() 交x轴负半轴于点N,交y轴于点M,且
交x轴负半轴于点N,交y轴于点M,且![]() .
.
(1)求抛物线![]() 的解析式与k的值;
的解析式与k的值;
(2)抛物线![]() 的对称轴交x轴于点D,连接
的对称轴交x轴于点D,连接![]() ,在x轴上方的对称轴上找一点E,使以点A,D,E为顶点的三角形与
,在x轴上方的对称轴上找一点E,使以点A,D,E为顶点的三角形与![]() 相似,求出
相似,求出![]() 的长;
的长;
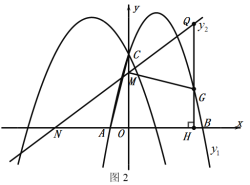
(3)如图2,过抛物线![]() 上的动点G作
上的动点G作![]() 轴于点H,交直线
轴于点H,交直线![]() 于点Q,若点
于点Q,若点![]() 是点Q关于直线
是点Q关于直线![]() 的对称点,是否存在点G(不与点C重合),使点
的对称点,是否存在点G(不与点C重合),使点![]() 落在y轴上?若存在,请直接写出点G的横坐标,若不存在,请说明理由.
落在y轴上?若存在,请直接写出点G的横坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,直线
中,直线![]() 分别交x轴、y轴于A,B两点,经过A,B两点的抛物线
分别交x轴、y轴于A,B两点,经过A,B两点的抛物线![]() 与x轴的正半轴相交于点
与x轴的正半轴相交于点![]() .
.

(1)求抛物线的解析式;
(2)若P为线段AB上一点,![]() ,求AP的长;
,求AP的长;
(3)在(2)的条件下,设M是y轴上一点,试问:抛物线上是否存在点N,使得以A,P,M,N为顶点的四边形为平行四边形?若存在,求出点N的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年,全球疫情大爆发,我国派遣医疗专家组对一些国家进行医疗援助,某批次派出20人组成的专家组,分别赴A、B、C、D四个国家开展援助工作,七人员分布情况如统计图(不完整)所示:
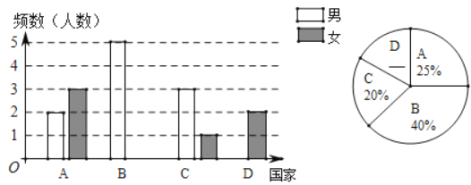
(1)计算赴B国女专家和D国男专家的人数,并将条形统计图补充完整;
(2)根据需要,从赴A国的专家,随机抽取两名专家对当地医疗团队进行培训,求所抽取的两名专家恰好是一男一女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,反比例函数
中,反比例函数![]() (
(![]() )的图象经过点
)的图象经过点![]() ,过点
,过点![]() 的直线
的直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于
轴分别交于![]() ,
,![]() 两点.
两点.

(1)求反比例函数的表达式;
(2)若![]() 的面积为
的面积为![]() 的面积的2倍,求此直线的函数表达式.
的面积的2倍,求此直线的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为推进“传统文化进校园”活动,某校准备成立“经典诵读”、“传统礼仪”、“民族器乐”和“地方戏曲”等四个课外活动小组.学生报名情况如图(每人只能选择一个小组):

(1)报名参加课外活动小组的学生共有 人,将条形图补充完整;
(2)扇形图中m= ,n= ;
(3)根据报名情况,学校决定从报名“经典诵读”小组的甲、乙、丙、丁四人中随机安排两人到“地方戏曲”小组,甲、乙恰好都被安排到“地方戏曲”小组的概率是多少?请用列表或画树状图的方法说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校举办“创建全国文明城市”知识竞赛,计划购买甲、乙两种奖品共30件.其中甲种奖品每件30元,乙种奖品每件20元.
(1)如果购买甲、乙两种奖品共花费800元,那么这两种奖品分别购买了多少件?
(2)若购买乙种奖品的件数不超过甲种奖品件数的3倍,如何购买甲、乙两种奖品,使得总花费最少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com