
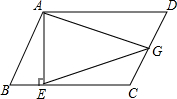
 已知:在?ABCD中,AE⊥BC,垂足为E,点G为CD上的中点,
已知:在?ABCD中,AE⊥BC,垂足为E,点G为CD上的中点,分析 (1)首先求出DC=AB=4,根据勾股定理求出BE即可;
(2)过G作GM⊥AE于M,利用平行线分线段成比例定理,求出M为AE中点,得出等腰三角形AGE,根据性质得出GM是∠AGE的角平分线,即可得出答案.
解答 (1)解:∵四边形ABCD是平行四边形,
∴AB=CD,
∵点G为CD的中点,CG=2,
∴DC=AB=4,
∵AE⊥BC,
∴∠AEB=90°,
在Rt△ABE中,由勾股定理得:BE=$\sqrt{{4}^{2}-{3}^{2}}$=$\sqrt{7}$;
(2)证明:过G作GM⊥AE于M,
∵AE⊥BE,GM⊥AE,
∴GM∥BC∥AD,
∴CG=DG,
∴AM=ME(一组平行线在一条直线上截得的线段相等,那么在另一条直线上截得的线段也相等),
∵GM⊥AE,
∴AG=EG,
∴∠AGM=∠EGM,
∴∠AGE=2∠MGE,
∵GM∥BC,
∴∠EGM=∠CEG,
∴∠CEG=$\frac{1}{2}$∠AGE.
点评 本题考查了平行四边形性质、等腰三角形的性质和判定、平行线分线段成比例定理、勾股定理等知识点的应用,得出AG=EG是解题关键.


科目:初中数学 来源: 题型:解答题
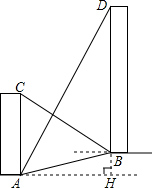 如图,AC、BD是一斜坡AB上的两幢楼房,斜坡AB的坡度是1:2$\sqrt{3}$,从点A测得楼BD顶部D处的仰角60°,从点B测得楼AC顶部C处的仰角30°,楼BD自身高度BD比楼AC高12米,求楼AC和楼BD之间的水平距离?(结果保留根号)
如图,AC、BD是一斜坡AB上的两幢楼房,斜坡AB的坡度是1:2$\sqrt{3}$,从点A测得楼BD顶部D处的仰角60°,从点B测得楼AC顶部C处的仰角30°,楼BD自身高度BD比楼AC高12米,求楼AC和楼BD之间的水平距离?(结果保留根号)查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知矩形ABCD中,AD=2AB,AB=6,E为AD中点,M为CD上一点,PE⊥EM交CB于点P,EN平分∠PEM交BC于点N.
已知矩形ABCD中,AD=2AB,AB=6,E为AD中点,M为CD上一点,PE⊥EM交CB于点P,EN平分∠PEM交BC于点N.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知抛物线经过A(-2,0),B(-3,3)及原点O,顶点为C
已知抛物线经过A(-2,0),B(-3,3)及原点O,顶点为C查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2.83×107吨 | B. | 2.83×108吨 | C. | 2.83×109吨 | D. | 2.83×1010吨 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com