
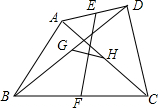
 如图,在四边形ABCD中,E、F分别是AD、BC的中点,G、H分别是BD、AC的中点,当AB、CD满足条件AB=CD时,有EF⊥GH.
如图,在四边形ABCD中,E、F分别是AD、BC的中点,G、H分别是BD、AC的中点,当AB、CD满足条件AB=CD时,有EF⊥GH. 分析 连接EG、GF、FH、HE,根据三角形中位线定理得到EG∥AB,EG=$\frac{1}{2}$AB,GF∥CD,GF=$\frac{1}{2}$CD,FH∥AB,FH=$\frac{1}{2}$AB,EH∥CD,EH=$\frac{1}{2}$CD,得到平行四边形EGFH,根据菱形的判定和性质证明结论.
解答 解:当AB=CD时,EF⊥GH.
利用: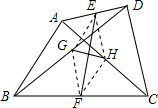 连接EG、GF、FH、HE,
连接EG、GF、FH、HE,
∵E、G分别是AD、BD的中点,
∴EG∥AB,EG=$\frac{1}{2}$AB,
同理GF∥CD,GF=$\frac{1}{2}$CD,FH∥AB,FH=$\frac{1}{2}$AB,EH∥CD,EH=$\frac{1}{2}$CD,
∴EG∥FH,EG=FH,
∴四边形EGFH是平行四边形,
当AB=CD时,EG=EH,
∴四边形EGFH是菱形,
∴EF⊥GH.
故答案为:AB=CD.
点评 本题考查的是三角形中位线定理的应用,平行四边形和菱形的判定,掌握三角形的中位线平行于第三边且等于第三边的一半和菱形的对角线互相垂直是解题的关键.


科目:初中数学 来源: 题型:解答题
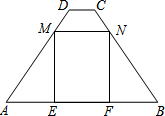 如图,在梯形ABCD中,AB∥CD,AB=7,CD=1,AD=BC=5.点M、N分别在边AD、BC上运动,并保持MN∥AB,ME⊥AB,NF⊥AB,垂足分别为E、F
如图,在梯形ABCD中,AB∥CD,AB=7,CD=1,AD=BC=5.点M、N分别在边AD、BC上运动,并保持MN∥AB,ME⊥AB,NF⊥AB,垂足分别为E、F查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y随x的增大而增大 | B. | 图象必经过点(-1,2) | ||
| C. | 图象在第二、四象限内 | D. | 若x>1,则-2<y<0 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在长方形ABCD中,AB>BC,BE⊥AC,垂足为E,延长BE交CD于F,S表示面积,则给出的下列命题:
如图,在长方形ABCD中,AB>BC,BE⊥AC,垂足为E,延长BE交CD于F,S表示面积,则给出的下列命题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
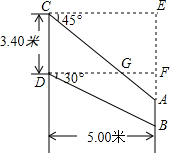 某型号飞机的机翼形状如图,根据图示尺寸计算AC和AB的长度(精确到0.1米,$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73 ).
某型号飞机的机翼形状如图,根据图示尺寸计算AC和AB的长度(精确到0.1米,$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73 ).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com