

 解:(1)猜想线段GF=GC,
解:(1)猜想线段GF=GC,


 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案科目:初中数学 来源: 题型:

| AD |
| AB |
| AD |
| AB |
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
 (1)操作发现:
(1)操作发现:查看答案和解析>>
科目:初中数学 来源:2011-2012年九年级上学期月考数学卷 题型:解答题
(1)操作发现:
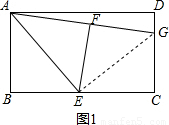
如图1,在矩形ABCD中,E是BC的中点,将△ABE沿AE折叠后得到△AFE,点F在矩形ABCD内部,延长AF交CD于点G.猜想线段GF与GC有何数量关系?并证明你的结论.
(2)类比探究:
如图2,将(1)中的矩形ABCD改为平行四边形,其它条件不变,(1)中的结论是否仍然成立?请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com