
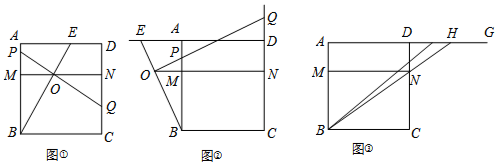
���� ��1����P��PF��CD��F�����PFQ=��BAE=90�㣬PF=AD=BA�����ж���QPF�ա�EBA��ASA���������ó�AE=FQ���ٸ���MP=NF��FQ=NF+NQ���ɵ�AE=MP+NQ��
��2����P��PF��CD��F�����PFQ=��BAE=90�㣬PF=AD=BA�����ж���PQF�ա�BEA��AAS���������ó�AE=FQ���ٸ���MP=NF��FQ=NQ-NF�����ɵó�AE=NQ-MP��
��3������ͼ�Σ��ɵõ���E���߶�DH��ʱ������AE=MP+NQ������E���߶�HG��ʱ������AE=MP-NQ��ͨ���������ߣ������ABE�ա�FPQ�����ɵó�AE=FQ���ٸ���MP=NF�����ɵõ�AE��MP��NQ֮���������ϵ��
���  �⣺��1��AE=MP+NQ��
�⣺��1��AE=MP+NQ��
֤������ͼ1����P��PF��CD��F�����PFQ=��BAE=90�㣬PF=AD=BA��
��OP��BE��PF��AB��
���QPF=��EBA��
�ڡ�QPF�͡�EBA�У�
$\left\{\begin{array}{l}{��PFQ=��BAE}\\{PF=BA}\\{��QPF=��EBA}\end{array}\right.$��
���QPF�ա�EBA��ASA����
��AE=FQ��
�֡�MP=NF��FQ=NF+NQ��
��AE=MP+NQ��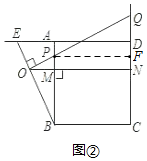
��2��AE=NQ-MP��
֤������ͼ2����P��PF��CD��F�����PFQ=��BAE=90�㣬PF=AD=BA��
��OP��BE��DQ��AD��
���PQF=��BEA��
�ڡ�PQF�͡�BEA�У�
$\left\{\begin{array}{l}{��PQF=��BEA}\\{��PFQ=��BAE}\\{PF=BA}\end{array}\right.$��
���PQF�ա�BEA��AAS����
��AE=FQ��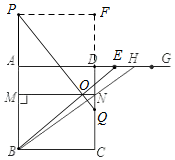
�֡�MP=NF��FQ=NQ-NF��
��AE=NQ-MP��
��3����ͼ��ʾ������E���߶�DH��ʱ������AE=MP+NQ��
���ɣ���P��PF��CD��F�����F=��BAE=90�㣬PF=AD=AB��
����OP��BE��CD��DE���ɵá�AEB=��FQP��
��֤��ABE�ա�FPQ��
��AE=FQ��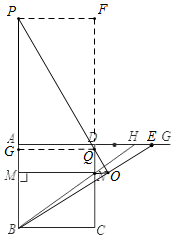
�֡�MP=NF��FQ=FN+NQ��
��AE=MP+NQ��
��ͼ��ʾ����E���߶�HG��ʱ������AE=MP-NQ��
���ɣ���P��PF��CD��F�����F=��BAE=90�㣬PF=AD=AB��
����OP��BE��CD��DE���ɵá�AEB=��FQP��
��֤��ABE�ա�FPQ��
��AE=FQ��
�֡�MP=NF��FQ=FN-NQ��
��AE=MP-NQ��
���� ���������ı����ۺ��⣬��Ҫ������ȫ�������ε��ж������ʣ����ε������Լ������ε����ʵ��ۺ����ã��������Ĺؼ����������ߣ�����ȫ�������Σ�����ȫ�������εĶ�Ӧ����ȣ����εĶԱ�����Լ��߶εĺͲ��ϵ�����Ƶ����㣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ij�̳�����һ���ڼ�Ϊ�����н����ۻ��������һ����������ת����ת�̣��̳��涨���˿���100Ԫ���Ͼ��ܻ��һ��ת��ת�̵Ļ��ᣬ��ת��ֹͣʱ��ָ��������һ����Ϳ��Ի����Ӧ�Ľ�Ʒ���±��Ǵ˴λ�е�һ��ͳ�����ݣ�
ij�̳�����һ���ڼ�Ϊ�����н����ۻ��������һ����������ת����ת�̣��̳��涨���˿���100Ԫ���Ͼ��ܻ��һ��ת��ת�̵Ļ��ᣬ��ת��ֹͣʱ��ָ��������һ����Ϳ��Ի����Ӧ�Ľ�Ʒ���±��Ǵ˴λ�е�һ��ͳ�����ݣ�| ת��ת�̵Ĵ���n | 100 | 200 | 400 | 500 | 800 | 1000 |
| ���ڡ����֡�����Ĵ���m | 60 | 122 | 240 | 298 | 476 | 604 |
| ���ڡ����֡������Ƶ��$\frac{m}{n}$ | 0.6 | 0.61 | 0.6 | 0.6 | 0.59 | 0.604 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
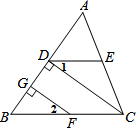 ��ͼ����֪FG��AB��CD��AB������ֱ�ΪG��D����1=��2��
��ͼ����֪FG��AB��CD��AB������ֱ�ΪG��D����1=��2���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��A=30�㡢��B=60�� | B�� | ��A=50�㡢��B=80�� | ||
| C�� | ��A=2��B=70�� | D�� | AB=4��BC=5���ܳ�Ϊ15 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com