
����Ŀ����ƽ��ֱ������ϵ�У�A(a��0)��C(0��c)�����㣺(a+6)2+![]() ��0��������ABCO������ϵ��(��ͼ)����OΪ����ϵ��ԭ�㣮
��0��������ABCO������ϵ��(��ͼ)����OΪ����ϵ��ԭ�㣮

(1)���B�����꣮
(2)��ͼ1������M�ӵ�A��������2����λ/����ٶ������˶�(��������O)����N��ԭ��O��������1����λ/����ٶ������˶�(��������C)����M��N����ͬʱ�������������˶��Ĺ����У��ı���MBNO������Ƿ����仯�������䣬����ֵ�����仯����仯�ķ�Χ��
(3)��ͼ2��EΪx�Ḻ������һ�㣬�ҡ�CBE����CEB��F��x����������һ���㣬��ECF��ƽ����CD��BE���ӳ����ڵ�D���ڵ�F�˶��Ĺ����У���̽����CFE���D��������ϵ����˵������
���𰸡�(1)B(��6����3)��(2)�ı���MBNO��������䣻�Ƕ�ֵ9��(3)��CFE��2��D.
��������
��1����������ɵ�a����6��c����3�������A�㣬C�㣬B�����ꣻ��2����M��Nͬʱ������ʱ��Ϊt����S�ı���MBNO��S������OABC��S��ABM��S��BCN��18��![]() ��2t��3��
��2t��3��![]() ��6����3��t����9����ʱ���أ�������Ƕ�ֵ����ֵΪ9����3�������������ڽǺͶ�������������ǵ��ڲ����ڵ������ڽǵĺͣ������CFE���D��������ϵ��
��6����3��t����9����ʱ���أ�������Ƕ�ֵ����ֵΪ9����3�������������ڽǺͶ�������������ǵ��ڲ����ڵ������ڽǵĺͣ������CFE���D��������ϵ��
�⣺(1)��(a+6)2+![]() ��0��
��0��
��a����6��c����3
��A(��6��0)��C(0����3)
���ı���OABC�Ǿ���
��AO��BC��AB��OC��AB��OC��3��AO��BC��6
��B(��6����3)
(2)�ı���MBNO��������䣮
��M��Nͬʱ������ʱ��Ϊt��
��S�ı���MBNO��S������OABC��S��ABM��S��BCN��18��![]() ��2t��3��
��2t��3��![]() ��6��(3��t)��9����ʱ���أ�
��6��(3��t)��9����ʱ���أ�
�����˶�������������䣮�Ƕ�ֵ9
(3)��CFE��2��D��
�������£���ͼ
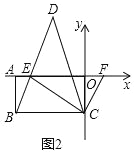
�ߡ�CBE����CEB
���ECB��180����2��BEC
��CDƽ�֡�ECF
���DCE����DCF
��AF��BC
���F��180������DCF����DCE����BCE��180����2��DCE��(180����2��BEC)
���F��2��BEC��2��DCE
�ߡ�BEC����D+��DCE
���F��2(��D+��DCE)��2��DCE
���F��2��D



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵxoy�У�A(-1,5)��B����1��0����C����4��3����
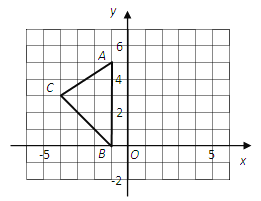
��1����ABC������� ��
��2������ͼ�л�����ABC����ƽ��2����λ������ƽ��5����λ��ġ�A1B1C1��
��3��д����A1��B1��C1�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ģ���ͼ��ֱ��AB��CD�ཻ�ڵ�O��OE��CD�ڵ�O��ODƽ�֡�BOF,��BOE=50![]() ��
��
���AOC����AOF����EOF�Ķ�����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˵������ȷ�ĸ�����( )
����![]() ����ȫƽ��ʽ����k=3
����ȫƽ��ʽ����k=3
�����̽����о������������εĽṹ���������������ξ����ȶ��Ե�����
�����������ڲ������߾�����ȵĵ��������ڽ�ƽ���ߵĽ���
����![]() ʱ
ʱ![]()
������P����AOB�ڲ���D��E�ֱ�����AOB���������ϣ�PD=PE,���P����AOB��ƽ������
A.1��B.2��C.3��D.4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̳��ƻ�һ���Թ���![]() ��
��![]() �����ͺ�ϴ�»�80̨��������
�����ͺ�ϴ�»�80̨��������![]() �ͺ�ϴ�»�50̨��
�ͺ�ϴ�»�50̨��![]() �ͺ�ϴ�»�30̨������55000Ԫ��������
�ͺ�ϴ�»�30̨������55000Ԫ��������![]() �ͺ�ϴ�»�30̨��
�ͺ�ϴ�»�30̨��![]() �ͺ�ϴ�»�50̨������6500Ԫ��
�ͺ�ϴ�»�50̨������6500Ԫ��
(1)��![]() ��
��![]() �����ͺŵ�ϴ�»��Ľ��۸�Ϊ����Ԫ��
�����ͺŵ�ϴ�»��Ľ��۸�Ϊ����Ԫ��
(2)��ÿ̨A�ͺ�ϴ�»��ۼ�550Ԫ��ÿ̨B�ͺ�ϴ�»��ۼ�1080Ԫ�����̳��ƻ���������80̨ϴ�»�����������5200Ԫ��������![]() �ͺ�ϴ�»�����̨��
�ͺ�ϴ�»�����̨��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������ͨ�¹ʷ�����������������ͨ�����Ϊ�ش�����������۶��������ѧ��ȤС��Ϊ����������ٶ����������ʵ������ͼ���ڹ�·MN�����ƿ���ֱ������ѡȡһ��C�����C����·�ľ���Ϊ30��������MN��ѡȡA��B�����������CAN=30������CBN=60����
��1����AB�ij�������ȷ��0.1�����ο�����![]() =1.41��
=1.41�� ![]() =1.73��
=1.73��
��2������·���������ٶ�Ϊ40ǧ��/Сʱ��ij����A��B��ʱ3�����ó��Ƿ��٣�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABC�У�AC��BC����ACB��90��������C��CD��AB�ڵ�D����E��AB����һ����(�����˵�A��B)������CE������B��CE�Ĵ��߽�ֱ��CE�ڵ�F����ֱ��CD�ڵ�G��

(1)��֤��AE��CG��
(2)����E�˶����߶�BD��ʱ(��ͼ��)���Բ���AE��CG��������ϵ�Ƿ����仯����֤����Ľ��ۣ�
(3)����A��AH��CE������Ϊ��H������CD���ӳ����ڵ�M(��ͼ��)���ҳ�ͼ����BE��ȵ��߶Σ�ֱ��д����BE=
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ֪��CD��AB�ڵ�O����EOF��90�㣬����OPƽ�֡�COF��
��1����ͼ1����EOF��ֱ��CD���Ҳࣺ
������COE��30�㣬���BOF�͡�POE�Ķ�����
�����жϡ�POE���BOP֮�����������������ϵ����˵�����ɣ�
��2����ͼ2����EOF��ֱ��CD����࣬�ҵ�E�ڵ�F���·���
����ֱ��д����POE���BOP֮���������ϵ��
����ֱ��д����POE���DOP֮���������ϵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ��������y= x2+bx+c��x�ᡢy��ֱ��ཻ�ڵ�A�� 1��0����B��0��3�����㣬�䶥��ΪD��
��1�������������ߵĽ���ʽ��
��2������������x�����һ������ΪE�� ���ODE������������ߵĶԳ������Ƿ���ڵ�Pʹ�á�PAB���ܳ���̡������������P������꣬��������˵�����ɡ�

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com