
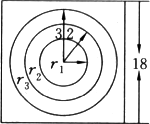
某馅饼店设有一个投镖靶,如图该靶为正方形板,边长为18厘米,挂于大门附近的墙上.顾客花伍角硬币便可投一镖,并有机会赢得三种意大利馅饼中的一个.投镖靶中画有三个同心圆,圆心在靶的中心,当投镖击中半径为1厘米的最内层圆形区域时,可得到一个大馅饼;当投镖击中半径为1厘米到2厘米之间的环形区域时,可得到一个中馅饼;当投镖击中半径为2厘米到3厘米之间的环形区域时,可得到一个小馅饼;如果击中靶上的其他部分,则得不到馅饼.我们假设每一个顾客都能投镖中靶,并假设每个圆的周边线没有宽度,即每次投镖不会击中线上,试求一顾客将赢得:(1)一张大馅饼的概率;(2)一张中馅饼的概率;(3)一张小馅饼的概率;(4)没得到馅饼的概率.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:中学学习一本通 数学 七年级下册 北师大课标 题型:044
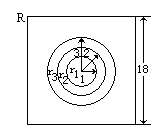
某馅饼店设有一个投镖靶(如图),该靶为正方形板,边长为18 cm,挂于大门附近的墙上.顾客花5角硬币便可投一镖并有机会赢得三种意大利馅饼中的一个.投镖靶中画有三个同心圆,圆心在靶的中心,当投镖击中半径1 cm的最内层圆形区域时,可得到一个大馅饼;当投镖击中半径为1 cm到2 cm之间的环域时,可得到一个中馅饼;当投镖击中半径为2 cm到3 cm之间的环域时,可得到一个小馅饼;如果击中靶上的其他部分,则得不到馅饼.我们假设每一个顾客都能投镖中靶,并假设每个圆的周边线没有宽度,即每个投镖者都不会击中线上,试求一顾客将赢得:(a)一张大馅饼;(b)一张中馅饼;(c)一张小馅饼;(d)没得到馅饼的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com