
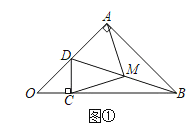
【题目】等腰直角三角形OAB中,∠OAB=90°,OA=AB,点D为OA中点,DC⊥OB,垂足为C,连接BD,点M为线段BD中点,连接AM、CM,如图①.

(1)求证:AM=CM;
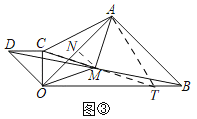
(2)将图①中的△OCD绕点O逆时针旋转90°,连接BD,点M为线段BD中点,连接AM、CM、OM,如图②.
①求证:AM=CM,AM⊥CM;
②若AB=4,求△AOM的面积.
【答案】(1)见解析;(2)①见解析,②2
【解析】
(1)直接利用直角三角形斜边的中线等于斜边的一半,即可得出结论;
(2)①延长CM交OB于T,先判断出△CDM≌△TBM得出CM=TM,DC=BT=OC,进而判断出△OAC≌△BAT,得出AC=AT,即可得出结论;
②先利用等腰直角三角形的性质求出再求出OD,DC=CO=![]() ,再用勾股定理得出CT,进而判断出CM=AM,得出AM=OM,进而求出ON,再根据勾股定理求出MN,即可得出结论.
,再用勾股定理得出CT,进而判断出CM=AM,得出AM=OM,进而求出ON,再根据勾股定理求出MN,即可得出结论.
解:(1)证明:∵∠OAB=90°,
∴△ABD是直角三角形,
∵点M是BD的中点,
∴AM=![]() BD,
BD,
∵DC⊥OB,
∴∠BCD=90°,
∵点M是BD的中点,
∴CM=![]() BD,
BD,
∴AM=CM;
(2)①如图②,
在图①中,∵AO=AB,∠OAB=90°,
∴∠ABO=∠AOB=45°,
∵DC⊥OB,
∴∠OCD=90°,
∴∠ODC=∠AOB,
∴OC=CD,
延长CM交OB于T,连接AT,
由旋转知,∠COB=90°,DC∥OB,
∴∠CDM=∠TBM,
∵点M是BD的中点,
∴DM=BM,
∵∠CMD=∠TMB,
∴△CDM≌△TBM(ASA),
∴CM=TM,DC=BT=OC,
∵∠AOC=∠BOC﹣∠AOB=45°=∠ABO,
∵AO=AB,
∴△OAC≌△BAT(SAS),
∴AC=AT,∠OAC=∠BAT,
∴∠CAT=∠OAC+∠OAT=∠BAT+∠OAT=∠OAB=90°,
∴△CAT是等腰直角三角形,
∵CM=TM,
∴AM⊥CM,AM=CM;
②如图③,在Rt△AOB中,AB=4,
∴OA=4,OB=![]() =
=![]() AB=4
AB=4![]() ,
,
在图①中,点D是OA的中点,
∴OD=![]() OA=2,
OA=2,
∵△OCD是等腰直角三角形,
∴DC=CO=ODsin45°=![]() =
=![]() ,
,
由①知,BT=CD,
∴BT=![]() ,
,
∴OT=OB﹣TB=3![]() ,
,
在Rt△OTC中,CT=![]() =2
=2![]() ,
,
∵CM=TM=![]() CT=
CT=![]() =AM,
=AM,
∵OM是Rt△COT的斜边上的中线,
∴OM=![]() CT=
CT=![]() ,
,
∴AM=OM,
过点M作MN⊥OA于N,则ON=AN=![]() OA=2,
OA=2,
根据勾股定理得,MN=![]() =1,
=1,
∴S△AOM=![]() OAMN=
OAMN=![]() ×4×1=2.
×4×1=2.



科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=![]() x2+bx+c经过△ABC的三个顶点,其中点A(0,1),点B(﹣9,10),AC∥x轴,点P是直线AC下方抛物线上的动点.
x2+bx+c经过△ABC的三个顶点,其中点A(0,1),点B(﹣9,10),AC∥x轴,点P是直线AC下方抛物线上的动点.
(1)求抛物线的解析式;(2)过点P且与y轴平行的直线l与直线AB、AC分别交于点E、F,当四边形AECP的面积最大时,求点P的坐标;
(3)当点P为抛物线的顶点时,在直线AC上是否存在点Q,使得以C、P、Q为顶点的三角形与△ABC相似,若存在,求出点Q的坐标,若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司组织退休职工组团前往某景点游览参观,参加人员共70人.旅游景点规定:①门票每人60元,无优惠;②上山游览必须乘坐景点安排的观光车游览,观光车有小型车和中型车两类,分别可供4名和11名乘客乘坐;且小型车每辆收费60元,中型车每人收费10元.若70人正好坐满每辆车且参观游览的总费用不超过5000元,问景点安排的小型车和中型车各多少辆?
查看答案和解析>>
科目:初中数学 来源: 题型:
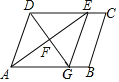
【题目】如图,四边形ABCD是平行四边形,AE平分∠BAD交CD于点E,AE的垂直平分线交AB于点G,交AE于点F.若AD=4cm,BG=1cm,则AB=_____cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,小红家阳台上放置了一个晒衣架.如图2是晒衣架的侧面示意图,立杆AB、CD相交于点O,B、D两点立于地面,经测量:AB=CD=136cm,OA=OC=51cm,OE=OF=34cm,现将晒衣架完全稳固张开,扣链EF成一条直线,且EF=32cm.
(1)求证:AC∥BD;
(2)求扣链EF与立杆AB的夹角∠OEF的度数(精确到0.1°);
(3)小红的连衣裙穿在衣架后的总长度达到122cm,垂挂在晒衣架上是否会拖落到地面?请通过计算说明理由.
(参考数据:sin61.9°≈0.882,cos61.9°≈0.471,tan61.9°≈0.553;可使用科学计算器)

查看答案和解析>>
科目:初中数学 来源: 题型:
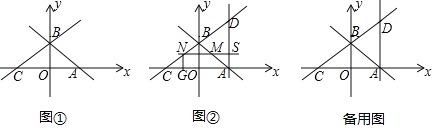
【题目】在平面直角坐标系xOy中,直线y=﹣x+2与x轴、y轴分别交于A、B两点,直线BC交x轴负半轴于点C,∠BCA=30°,如图①.
(1)求直线BC的解析式.
(2)在图①中,过点A作x轴的垂线交直线CB于点D,若动点M从点A出发,沿射线AB方向以每秒![]() 个单位长度的速度运动,同时,动点N从点C出发,沿射线CB方向以每秒2个单位长度的速度运动,直线MN与直线AD交于点S,如图②,设运动时间为t秒,当△DSN≌△BOC时,求t的值.
个单位长度的速度运动,同时,动点N从点C出发,沿射线CB方向以每秒2个单位长度的速度运动,直线MN与直线AD交于点S,如图②,设运动时间为t秒,当△DSN≌△BOC时,求t的值.
(3)若点M是直线AB在第二象限上的一点,点N、P分别在直线BC、直线AD上,是否存在以M、B、N、P为顶点的四边形是菱形.若存在,请直接写出点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
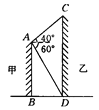
【题目】如图所示,两建筑物的水平距离为24 m,从A点测得D点的俯角为60°,测得C点的仰角为40°,求这两座建筑物的高.(![]() ≈1.732,tan 40°≈0.8391,精确到0.01 m)
≈1.732,tan 40°≈0.8391,精确到0.01 m)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与探究如图,直线![]() 的解析式为
的解析式为![]() ,且
,且![]() 与
与![]() 轴交于点
轴交于点![]() ,直线
,直线![]() 经过点
经过点![]() 和点
和点![]() ,直线
,直线![]() ,
,![]() 交于点
交于点![]() ,连接
,连接![]() .
.
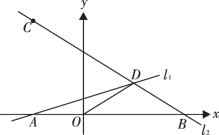
(1)求直线![]() 的解析式;
的解析式;
(2)求证:![]() 是等腰三角形;
是等腰三角形;
(3)求![]() 的面积;
的面积;
(4)探究在直线![]() 上是否存在异于点
上是否存在异于点![]() 的另一点
的另一点![]() ,使得
,使得![]() 与
与![]() 的面积相等,若存在,请直接写出点
的面积相等,若存在,请直接写出点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com