
【题目】一盒中有x个黑球和2个白球,这些球除颜色外无其他差别.若从盒中随机取一个球,黑球的概率是 ![]() .
.
(1)填空:x=;
(2)从该盒子中随机摸出一个球,记下颜色后,不放回,再从该盒子中摸出一个球记下颜色,请用画树状图或列表求两次摸出的球的颜色都是白色的概率.
【答案】
(1)3
(2)解:画出树状图如下:
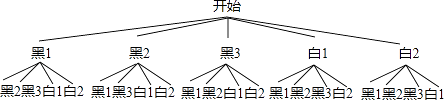
共有20种情况,其中两次摸出的球的颜色都是白色的有2种情况,
所以,P(两次摸出的球的颜色都是白色)= ![]() =
= ![]()
【解析】解:(1)∵黑球的概率是 ![]() ,
,
∴ ![]() =
= ![]() ,
,
解得x=3;
(2)画出树状图如下:

共有20种情况,其中两次摸出的球的颜色都是白色的有2种情况,
所以,P(两次摸出的球的颜色都是白色)= ![]() =
= ![]()
所以答案是:(1)3;(2)![]() .
.
【考点精析】通过灵活运用列表法与树状图法和概率公式,掌握当一次试验要设计三个或更多的因素时,用列表法就不方便了,为了不重不漏地列出所有可能的结果,通常采用树状图法求概率;一般地,如果在一次试验中,有n种可能的结果,并且它们发生的可能性都相等,事件A包含其中的m中结果,那么事件A发生的概率为P(A)=m/n即可以解答此题.


科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b与反比例函数 ![]() 的图象交于A(m,6),B(3,n)两点.
的图象交于A(m,6),B(3,n)两点. 
(1)求一次函数的解析式;
(2)根据图象直接写出 ![]() 的x的取值范围;
的x的取值范围;
(3)求△AOB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=x2+bx+c与x轴交于点A,B,与y轴交于点C,其中点A在y轴的左侧,点C在x轴的下方,且OA=OC=5.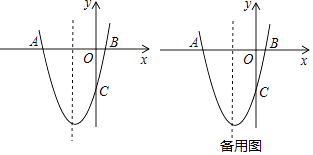
(1)求抛物线对应的函数解析式;
(2)点P为抛物线对称轴上的一动点,当PB+PC的值最小时,求点P的坐标;
(3)在(2)条件下,点E为抛物线的对称轴上的动点,点F为抛物线上的动点,以点P、E、F为顶点作四边形PEFM,当四边形PEFM为正方形时,请直接写出坐标为整数的点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(7分)为倡导节约用电,某地决定对居民家庭用电实行“阶梯电价”,电力公司规定:居民家庭每月用电量在80千瓦时以下(含80千瓦时,1千瓦时俗称1度)时,实行“基本电价”;当居民家庭月用电量超过80千瓦时时,超过部分实行“提高电价”.
(1)(4分)小张家2015年2月份用电100千瓦时,上缴电费68元;3月份用电120千瓦时,上缴电费88元.问“基本电价”和“提高电价”分别为多少元/千瓦时?
(2)(3分)若4月份小张家预计用电130千瓦时,请预算小张家4月份应上缴的电费.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近期电视剧《人民的名义》热播,某校“话剧表演”社团在本校学生中开展学生知晓情况专题调查活动,采取随机抽样的方式进行问卷调查,问卷调查的结果分为A,B,C,D四类.其中,A类表示“自己看过”,B类表示“听家长讲过”,
C类表示“听同学讲过”,D类表示“不知道”,划分类别后的数据整理如表:
类别 | A | B | C | D |
频数 | 30 | 40 | 24 | b |
频率 | a | 0.4 | 0.24 | 0.06 |
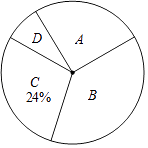
(1)表中的a=b=;
(2)根据表中数据,求扇形统计图中类别为B的学生数所对应的扇形圆心角的度数;
(3)若该校有学生1000名,根据调查结果估计该校学生中类别为C的人数约为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】自4月以来,我市推出了一项“共享单车”的便民举措,为人们的城市生活出行带来了方便.图(1)所示的是某款单车的实物图.图(2)是这辆单车的部分几何示意图,其中车支架BC的长为20cm,且∠CBA=75°,∠CAB=30°.求车架档AB的长.(参考数据:sin75°= ![]() ,cos75°=
,cos75°= ![]() ,tan75°=2+
,tan75°=2+ ![]() )
)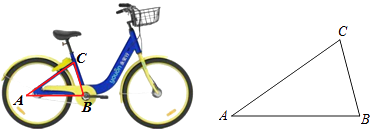
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“单词的记忆效率“是指复习一定量的单词,一周后能正确默写出的单词个数与复习的单词个数的比值.如图描述了某次单词复习中小华,小红小刚和小强四位同学的单词记忆效率y与复习的单词个数x的情况,则这四位同学在这次单词复习中正确默写出的单词个数最多的是( )

A. 小华B. 小红C. 小刚D. 小强
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下面的证明过程:
如图所示,直线AD与AB,CD分别相交于点A,D,与EC,BF分别相交于点H,G,已知∠1=∠2,∠B=∠C.
求证:∠A=∠D.
证明:∵∠1=∠2,(已知)∠2=∠AGB( )
∴∠1= ( )
∴EC∥BF( )
∴∠B=∠AEC( )
又∵∠B=∠C(已知)
∴∠AEC= ( )
∴ ( )
∴∠A=∠D( )

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com