
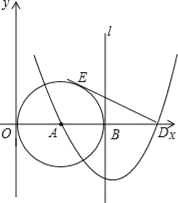
【题目】如图,已知点A(3,0),以A为圆心作⊙A与Y轴切于原点,与x轴的另一个交点为B,过B作⊙A的切线l.
(1)以直线l为对称轴的抛物线过点A及点C(0,9),求此抛物线的解析式;
(2)抛物线与x轴的另一个交点为D,过D作⊙A的切线DE,E为切点,求此切线长;
(3)点F是切线DE上的一个动点,当△BFD与△EAD相似时,求出BF的长.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 或
或![]() .
.
【解析】
试题(1)已知了抛物线的顶点坐标,可将抛物线的解析式设为顶点坐标式,然后将C点坐标代入求解即可.
(2)由于DE是⊙A的切线,连接AE,那么根据切线的性质知AE⊥DE,在Rt△AED中,AE、AB是圆的半径,即AE=OA=AB=3,而A、D关于抛物线的对称轴对称,即AB=BD=3,由此可得到AD的长,进而可利用勾股定理求得切线DE的长.
(3)若△BFD与EAD△相似,则有两种情况需要考虑:①△AED∽△BFD,②△AED∽△FBD,根据不同的相似三角形所得不同的比例线段即可求得BF的长.
试题解析:(1)设抛物线的解析式为y=a(x-6)2+k;
∵抛物线经过点A(3,0)和C(0,9),
∴![]() ,
,
解得: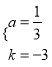
∴y=![]() (x-6)2-3.
(x-6)2-3.
(2)连接AE;
∵DE是⊙A的切线,
∴∠AED=90°,AE=3,
∵直线l是抛物线的对称轴,点A,D是抛物线与x轴的交点,
∴AB=BD=3,
∴AD=6;
在Rt△ADE中,DE2=AD2-AE2=62-32=27,
∴DE=3![]() .
.
(3)当BF⊥ED时;
∵∠AED=∠BFD=90°,∠ADE=∠BDF,
∴△AED∽△BFD,
∴![]() ,
,
即![]() ,
,
∴BF=![]() ;
;
当FB⊥AD时,
∵∠AED=∠FBD=90°,∠ADE=∠FDB,
∴△AED∽△FBD,
∴![]() ,
,
即BF=![]() ;
;
∴BF的长为![]() 或
或![]() .
.



科目:初中数学 来源: 题型:
【题目】如图,△OAP是等腰直角三角形,∠OAP=90°,点A在第四象限,点P坐标为(8,0),抛物线y=ax2+bx+c经过原点O和A、P两点.
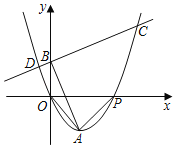
(1)求抛物线的函数关系式.
(2)点B是y轴正半轴上一点,连接AB,过点B作AB的垂线交抛物线于C、D两点,且BC=AB,求点B坐标;
(3)在(2)的条件下,点M是线段BC上一点,过点M作x轴的垂线交抛物线于点N,求△CBN面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
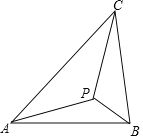
【题目】如图示,若△ABC内一点P满足∠PAC=∠PBA=∠PCB,则点P为△ABC的布洛卡点.三角形的布洛卡点(Brocard point)是法国数学家和数学教育家克洛尔(A.L.Crelle 1780﹣1855)于1816年首次发现,但他的发现并未被当时的人们所注意,1875年,布洛卡点被一个数学爱好者法国军官布洛卡(Brocard 1845﹣1922)重新发现,并用他的名字命名.问题:已知在等腰直角三角形DEF中,∠EDF=90°,若点Q为△DEF的布洛卡点,DQ=1,则EQ+FQ=( )
A.5 B.4 C.3+![]() D.2+
D.2+![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知反比例函数![]() 的图象与一次函数
的图象与一次函数![]() 的图象相交于点A(1,4)和点B(n,
的图象相交于点A(1,4)和点B(n,![]() ).
).
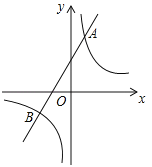
(1)求反比例函数和一次函数的解析式;
(2)当一次函数的值小于反比例函数的值时,直接写出x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2011年国家对“酒后驾车”加大了处罚力度,出台了不准酒后驾车的禁令,某记者在一停车场对开车的司机进行了相关的调查,本次调查结果共有四种情况:①有时会喝点酒开车;②已戒酒或从不喝酒;③酒后不开车或请专业司机代驾;④平时喝酒,但开车当天不喝酒.将这次调查情况整理并绘制成如下尚不完整的统计图,请根据相关信息,解答下列问题.
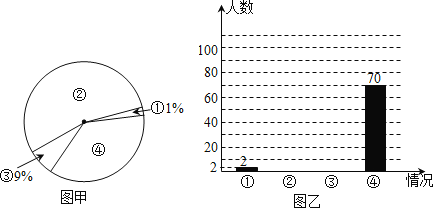
(1)该记者本次一共调查
了 名司机.
(2)求图①中④所在扇形的圆心角,并补全图②.
(3)在本次调查中,记者随机采访其中一名司机,求他属于第②种情况的概率.
(4)请估计在开车的10万名司机中,违反“酒驾”禁令的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解不等式组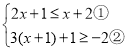 请结合题意填空,完成本题的解答.
请结合题意填空,完成本题的解答.
(Ⅰ)解不等式①,得____________________;
(Ⅱ)解不等式②,得_______________________;
(III)把不等式①和②的解集在数轴上表示出来:

(IV)原不等式组的解集为________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△PMN中,∠P=90°,PM=PN,MN=6cm,矩形ABCD中AB=2cm,BC=10cm,点C和点M重合,点B、C(M)、N在同一直线上,令Rt△PMN不动,矩形ABCD沿MN所在直线以每秒1cm的速度向右移动,至点C与点N重合为止,设移动x秒后,矩形ABCD与△PMN重叠部分的面积为y,则y与x的大致图象是( )
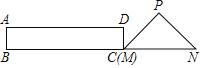
A. 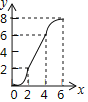 B.
B. 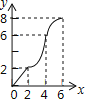 C.
C. 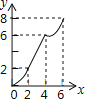 D.
D. 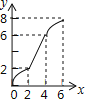
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=4,BC=6,点M是BC的中点.
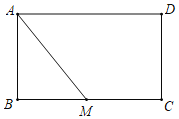
(1)在AM上求作一点E,使△ADE∽△MAB(尺规作图,不写作法);
(2)在(1)的条件下,求AE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com