练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    5．已知x-y=2，xy=-1，则（1+2x）（1-2y）的值为9．

    分析 原式利用多项式乘以多项式法则计算，整理后将已知等式代入计算即可求出值．

    解答 解：∵x-y=2，xy=-1，
    ∴原式=1+2（x-y）-4xy=1+4+4=9，
    故答案为：9

    点评 此题考查了整式的混合运算-化简求值，熟练掌握运算法则是解本题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    13．若$\sqrt{3x+1}$在实数范围内有意义，则x的取值范围是（　　）
    A．x$＞\frac{1}{3}$B．x≥$\frac{1}{3}$C．x≥-$\frac{1}{3}$D．x＞-$\frac{1}{3}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

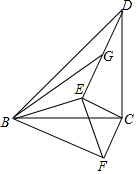    16．如图，在等腰直角△BCD中，∠BCD=90°，BC=CD，E为△BCD内一点，且CE⊥DE，DE=2CE，将△CDE绕点C逆时针旋转90°得到△CBF，连接EF、BE，G为DE的中点，连接BG．如果△BDG的面积为1cm2，那么BG的长度为$\sqrt{10}$cm．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    13．一个三角形的两边相等，一边长为3，另一边长为6，则这个三角形的周长是15．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    20．如图是甲，乙两人在一次追击游戏中的图象，就图中的数据，用你自己的语言设计一道应用题，并作出解答过程（图中S表示距离，t表示时间）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

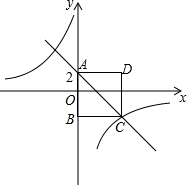    10．如图，四边形ABCD为正方形．点A的坐标为（0，2），点B的坐标为（0，-3）．反比例函数y=$\frac{k}{x}$图象经过点C，一次函数y=ax+b的图象经过点A、C．
    （1）求反比例函数与一次函数的解析式；
    （2）观察图象，直接写出在第四项限内使得$\frac{k}{x}$＜ax+b成立的自变量x的取值范围；
    （3）若点P是反比例函数图象上的一点，且△OAP的面积恰好等于正方形ABCD的面积，求P点的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    17．下列说法中正确的是（　　）
    A．“打开电视，正在播放《动物世界》”是必然事件
    B．某种彩票的中奖概率为$\frac{1}{1000}$，说明每买1000张彩票，一定有一张中奖
    C．抛掷一枚质地均匀的硬币一次，出现正面朝上的概率为$\frac{1}{2}$
    D．投掷两枚普通的正方体骰子，掷得两个6的概率是$\frac{1}{12}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    14．如图，将一副三角尺的直角顶点O重合，摆放在桌面上，若∠AOD=156°，则∠BOC=24°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

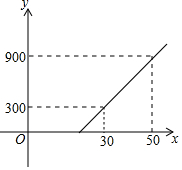    15．某旅客携带x（公斤）的行李乘飞机，登机前，旅客可选择托运或快递行李，托运费y1（元）与行李质量x（公斤）的对应关系由如图所示的一次函数图象确定，下表列出了快递费y2（元）与行李质量x（公斤）的对应关系，
    行李的质量x（公斤）快递费
    不超过1公斤10元
    超过1公斤但不超过5公斤的部分3元/公斤
    超过5公斤但不超过15公斤的部分5元/公斤
    （1）如果旅客选择托运，求可携带的免费行李的最大质量为多少公斤？
    （2）如果旅客选择快递，当1≤x≤15时，求快递费y2（元）与行李质量x（公斤）的函数关系式；
    （3）某旅客携带25公斤的行李，设托运m（公斤）行李（10≤m＜24，m为正整数），剩下的行李选择快递，m为何值时，总费用y的值最小，总费用的最小值是多少？

    查看答案和解析>>

    同步练习册答案