
 如图,在反比例函数y=$\frac{4}{x}$(x>0)的图象上,有点P1,P2,P3,P4…Pn(n为正整数,且n≥1).它们的横坐标依次为1,2,3,4…n(n为正整数,且n≥1),分别过这些点作x轴与y轴的垂线,连接相邻两点,图中所构成的阴影部分的面积从左到右依次为S1,S2,S3…Sn-1(n为正整数,且n≥2),那么S2+S3+S4+…S7=$\frac{3}{4}$.
如图,在反比例函数y=$\frac{4}{x}$(x>0)的图象上,有点P1,P2,P3,P4…Pn(n为正整数,且n≥1).它们的横坐标依次为1,2,3,4…n(n为正整数,且n≥1),分别过这些点作x轴与y轴的垂线,连接相邻两点,图中所构成的阴影部分的面积从左到右依次为S1,S2,S3…Sn-1(n为正整数,且n≥2),那么S2+S3+S4+…S7=$\frac{3}{4}$. 分析 求出P1、P2、P3、P4…的纵坐标,从而可计算出S1、S2、S3、S4…的高,进而求出S1、S2、S3、S4…,从而得出S2+S3+…+S7的值.
解答 解:当x=1时,P1的纵坐标为4,
当x=2时,P2的纵坐标为2,
当x=3时,P3的纵坐标为$\frac{4}{3}$,
当x=4时,P4的纵坐标为1,
当x=5时,P5的纵坐标为$\frac{4}{5}$,
…
则S1=$\frac{1}{2}$×1×(4-2)=1=2-1;
S2=$\frac{1}{2}$×1×(2-$\frac{4}{3}$)=$\frac{1}{3}$=1-$\frac{2}{3}$;
S3=$\frac{1}{2}$×1×($\frac{4}{3}$-1)=$\frac{1}{6}$=$\frac{2}{3}$-$\frac{2}{4}$;
S4=$\frac{1}{2}$×1×(1-$\frac{4}{5}$)=$\frac{1}{10}$=$\frac{2}{4}$-$\frac{2}{5}$;
…
Sn=$\frac{2}{n}$-$\frac{2}{n+1}$;
∴S2+S3+S4+…+S7
=1-$\frac{2}{3}$+$\frac{2}{3}$-$\frac{2}{4}$+…+$\frac{2}{7}$-$\frac{2}{8}$
=1-$\frac{1}{4}$
=$\frac{3}{4}$,
故答案为:$\frac{3}{4}$.
点评 此题考查了反比例函数图象上点的坐标特征,根据坐标求出个阴影的面积表达式是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
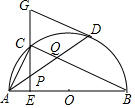 如图,在⊙O中,AB是直径,点D是⊙O上一点,点C是弧AD的中点,弦CE⊥AB于点E,过点D的切线交EC的延长线于点G,连接AD,分别交CE、CB于点P、Q,连接AC,给出下列结论:①∠DAC=∠ABC;②AD=CB;③点P是△ACQ的外心;④AC2=AE•AB;⑤CB∥GD,其中正确的结论是( )
如图,在⊙O中,AB是直径,点D是⊙O上一点,点C是弧AD的中点,弦CE⊥AB于点E,过点D的切线交EC的延长线于点G,连接AD,分别交CE、CB于点P、Q,连接AC,给出下列结论:①∠DAC=∠ABC;②AD=CB;③点P是△ACQ的外心;④AC2=AE•AB;⑤CB∥GD,其中正确的结论是( )| A. | ①③⑤ | B. | ②④⑤ | C. | ①②⑤ | D. | ①③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a=2,b=3 | B. | a=-2,b=-3 | C. | a=-2,b=3 | D. | a=2,b=-3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com