
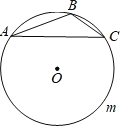
【题目】如图,△ABC中,∠ABC=120°,AC=2,⊙O是△ABC的外接圆,D是![]() 上任意一点(不包括点A、C),顺次连接四边形ABCD四边中点得到四边形EFGH,则四边形EFGH的周长的最大值为____________.
上任意一点(不包括点A、C),顺次连接四边形ABCD四边中点得到四边形EFGH,则四边形EFGH的周长的最大值为____________.
【答案】![]() .
.
【解析】
根据圆内接四边形的性质得到∠D=60°,连接OA,OC,过O作OM⊥AC于M,解直角三角形求出OA的值,如图2,四边形EFGH是边形ABCD的中点四边形,根据三角形的中位线的性质得到EF=HG=![]() AC,EH=FG=
AC,EH=FG=![]() BD,于是得到结论.
BD,于是得到结论.
如图1.
∵四边形ABCD 是圆内接四边形,∠ABC=120°,∴∠D=60°,
连接OA,OC,∴∠AOC=120°,
过O作OM⊥AC于M,
∴∠AOM![]() AOC=60°,AM
AOC=60°,AM![]() AC=1,
AC=1,
∴OA![]() ,
,
∴BD![]() .
.
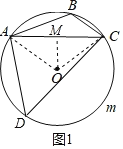
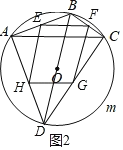
如图2,四边形EFGH是边形ABCD的中点四边形,
∴EF=HG![]() AC,EH=FG
AC,EH=FG![]() BD,
BD,
∴当BD最大时,四边形EFGH的周长的值最大,
∴当BD为⊙O的直径时,四边形EFGH的周长的值最大,
∴四边形EFGH的周长的最大值=EF+HG+HE+GF=AC+BD=2![]() .
.
故答案为:2![]() .
.


科目:初中数学 来源: 题型:
【题目】一粒木质中国象棋子“兵”,它的正面雕刻一个“兵”字,它的反面是平的![]() 将它从一定高度下掷,落地反弹后可能是“兵”字面朝上,也可能是“兵”字面朝下
将它从一定高度下掷,落地反弹后可能是“兵”字面朝上,也可能是“兵”字面朝下![]() 由于棋子的两面不均匀,为了估计“兵”字面朝上的概率,某实验小组做了棋子下掷实验,实验数据如下表:
由于棋子的两面不均匀,为了估计“兵”字面朝上的概率,某实验小组做了棋子下掷实验,实验数据如下表:
实验次数n | 20 | 60 | 100 | 120 | 140 | 160 | 500 | 1000 | 2000 | 5000 |
“兵”字面朝上次数m | 14 | 38 | 52 | 66 | 78 | 88 | 280 | 550 | 1100 | 2750 |
“兵”字面朝上频率 |
|
|
|
|
|
|
|
|
|
|
下面有三个推断:![]() 投掷1000次时,“兵”字面朝上的次数是550,所以“兵”字面朝上的概率是
投掷1000次时,“兵”字面朝上的次数是550,所以“兵”字面朝上的概率是![]() ;
;![]() 随着实验次数的增加,“兵”字面朝上的频率总在
随着实验次数的增加,“兵”字面朝上的频率总在![]() 附近,显示出一定的稳定性,可以估计“兵”字面朝上的概率是
附近,显示出一定的稳定性,可以估计“兵”字面朝上的概率是![]() ;
;![]() 当实验次数为200次时,“兵”字面朝上的频率一定是
当实验次数为200次时,“兵”字面朝上的频率一定是![]() 其中合理的是
其中合理的是![]()
![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
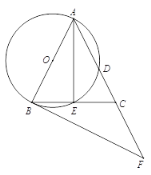
【题目】如图,在△ABC 中,AB = AC,以AB为直径的⊙O 分 别交AC,BC于点 D,E,过点B作⊙O的切线, 交 AC的延长线于点F.
(1) 求证:∠CBF =![]() ∠CAB;
∠CAB;
(2) 若CD = 2,![]() ,求FC的长.
,求FC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
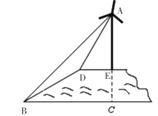
【题目】随着传统的石油、煤等自然资源逐渐消耗殆尽,风力、核能、水电等一批新能源被广泛使用.现在山顶的一块平地![]() 上建有一座风车
上建有一座风车![]() ,山的斜坡
,山的斜坡![]() 的坡度
的坡度![]() ,长是100米,在山坡的坡底
,长是100米,在山坡的坡底![]() 处测得风车顶端
处测得风车顶端![]() 的仰角为
的仰角为![]() ,在山坡的坡顶
,在山坡的坡顶![]() 处测得风车顶端
处测得风车顶端![]() 的仰角为
的仰角为![]() ,请你计算风车的高度.(结果保留根号)
,请你计算风车的高度.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】山西省每年的体育考试分成必考科目与选考科目两部分.其中选考科目是从一分钟跳绳、掷实心球、坐位体前屈、仰卧起坐四个项目中选取一项.王红与李丽是一对好朋友且都在2020年参加中考,实心球是她俩的弱项,其他三项都非常强,体育考试选考的四个项目中,她俩一定不会选实心球.
(1)王红在选考项目中,选中坐位体前屈的概率是 .
(2)王红与李丽选取同一个选考项目的概率是多少? (在画树状图或列表时,“一分钟跳绳"用“![]() ”表示,“坐位体前屈”用“
”表示,“坐位体前屈”用“![]() "表示,“仰卧起坐”用“
"表示,“仰卧起坐”用“![]() ”表示,“掷实心球”用“
”表示,“掷实心球”用“![]() ”表示)
”表示)
(3)通过对我省某市2020年参加中考的学生进行随机调查,发现该市选择“坐位体前屈”的学生的频率稳定在![]() 左右,已知该市有
左右,已知该市有![]() 人参加2020年中考体育,请由此估计该市这
人参加2020年中考体育,请由此估计该市这![]() 名学生中选择“坐位体前屈”的人数.
名学生中选择“坐位体前屈”的人数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=(x﹣m)(x﹣m﹣4)(m为常数).
(1)求证:不论m为何值,该函数的图象与x轴总有两个不同的公共点;
(2)求证:不论m为何值,该函数的图象的顶点纵坐标不变;
(3)若该函数的图象与x轴交点为A、B,与y轴交点为C,当﹣3≤m≤﹣1时,△ABC面积S的取值范围为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,![]() 内接于⊙O,过C作射线CP与BA的延长线交于点P,
内接于⊙O,过C作射线CP与BA的延长线交于点P,![]() .
.

(1)求证:CP是⊙O的切线;
(2)若![]() ,
,![]() ,求AB的长;
,求AB的长;
(3)如图2,D是BC的中点,PD与AC交于点E,求证:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,CD是AB边上的高,若
,CD是AB边上的高,若![]() .
.

(1)求CD的长.
(2)动点P在边AB上从点A出发向点B运动,速度为1个单位/秒;动点Q在边AC上从点A出发向点C运动,速度为v个单位秒![]() ,设运动的时间为
,设运动的时间为![]() ,当点Q到点C时,两个点都停止运动.
,当点Q到点C时,两个点都停止运动.
①若当![]() 时,
时,![]() ,求t的值.
,求t的值.
②若在运动过程中存在某一时刻,使![]() 成立,求v关于t的函数表达式,并写出自变量t的取值范围.
成立,求v关于t的函数表达式,并写出自变量t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与探究:
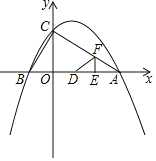
已知二次函数y=﹣![]() x2+
x2+![]() x+2的图象与x轴交于A,B两点(点B在点A的左侧),与y轴交于点C.
x+2的图象与x轴交于A,B两点(点B在点A的左侧),与y轴交于点C.
(1)求点A,B,C的坐标;
(2)求证:△ABC为直角三角形;
(3)如图,动点E,F同时从点A出发,其中点E以每秒2个单位长度的速度沿AB边向终点B运动,点F以每秒![]() 个单位长度的速度沿射线AC方向运动.当点F停止运动时,点E随之停止运动.设运动时间为t秒,连结EF,将△AEF沿EF翻折,使点A落在点D处,得到△DEF.当点F在AC上时,是否存在某一时刻t,使得△DCO≌△BCO?(点D不与点B重合)若存在,求出t的值;若不存在,请说明理由.
个单位长度的速度沿射线AC方向运动.当点F停止运动时,点E随之停止运动.设运动时间为t秒,连结EF,将△AEF沿EF翻折,使点A落在点D处,得到△DEF.当点F在AC上时,是否存在某一时刻t,使得△DCO≌△BCO?(点D不与点B重合)若存在,求出t的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com