
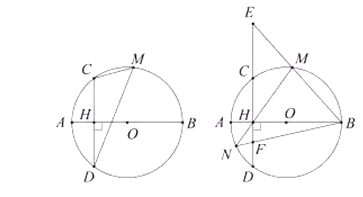
【题目】如图,线段 ![]() 是
是 ![]() 的直径,弦
的直径,弦 ![]() 于点
于点 ![]() ,点
,点 ![]() 是弧
是弧 ![]() 上任意一点,
上任意一点, ![]() .
.
(1)求 ![]() 的半径
的半径 ![]() 的长度;
的长度;
(2)求 ![]() ;
;
(3)直线 ![]() 交直线
交直线 ![]() 于点
于点 ![]() ,直线
,直线 ![]() 交
交 ![]() 于点
于点 ![]() ,连接
,连接 ![]() 交
交 ![]() 于点
于点 ![]() ,求
,求 ![]() 的值.
的值.
【答案】
(1)
解:连接OC,在Rt△COH中,
∵CH=4,OH=r-2,OC=r.
∴ (r-2)2+42=r2.
∴ r=5
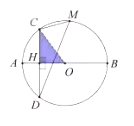
(2)
解:∵弦CD与直径AB垂直,
∴ 弧AD=弧AC=![]() 弧CD.
弧CD.
∴ ∠AOC=![]() ∠COD.
∠COD.
∴∠CMD=![]() ∠COD.
∠COD.
∴ ∠CMD=∠AOC.
∴sin∠CMD=sin∠AOC.
在Rt△COH中,
∴sin∠AOC=![]() =
=![]() .
.
∴sin∠CMD=![]() .
.
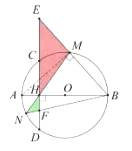
(3)
解:连接AM,
∴∠AMB=90°.
在Rt△AMB中,
∴∠MAB+∠ABM=90°.
在Rt△EHB中,
∴∠E+∠ABM=90°.
∴∠MAB=∠E.
∵弧BM=弧BM,
∴∠MNB=∠MAB=∠E.
∵∠EHM=∠NHF.
∴△EHM∽△NHF
∴![]() =
=![]() .
.
∴HE.HF=HM.HN.
∵AB与MN交于点H,
∴HM.HN=HA.HB=HA.(2r-HA)=2×(10-2)=16.
∴HE.HF=16.
【解析】(1)连接OC,在Rt△COH中,根据勾股定理即可r.
(2)根据垂径定理即可得出弧AD=弧AC=![]() 弧CD;再根据同弧所对的圆周角等于圆心角的一半;得出 ∠CMD=∠AOC;在Rt△COH中,根据锐角三角函数定义即可得出答案.
弧CD;再根据同弧所对的圆周角等于圆心角的一半;得出 ∠CMD=∠AOC;在Rt△COH中,根据锐角三角函数定义即可得出答案.
(3)连接AM,则∠AMB=90°.在Rt△AMB中和Rt△EHB中,根据同角的余角相等即可∠MAB=∠E;再由三角形相似的判定和性质即可得HE.HF=HM.HN.
又由AB与MN交于点H,得出HM.HN=HA.HB=HA.(2r-HA)=2×(10-2)=16;从而求出HE.HF=16.
【考点精析】关于本题考查的余角和补角的特征和勾股定理的概念,需要了解互余、互补是指两个角的数量关系,与两个角的位置无关;直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2才能得出正确答案.


科目:初中数学 来源: 题型:
【题目】根据给出的图形回答下列问题:
(1)∠1表示成∠A,这样的表示方法是否正确?如果不正确,应该怎样改正?
(2)图中哪个角可以用一个字母来表示?
(3)以A为顶点的角有几个?请表示出来;
(4)∠ADC与∠ACD是同一个角吗?请说明理由.
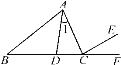
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是“经过已知直线外一点作这条直线的垂线”的尺规作图过程:
已知:直线l和l外一点P.(如图1)
求作:直线l的垂线,使它经过点P.
作法:如图2
(1)在直线l上任取两点A,B;
(2)分别以点A,B为圆心,AP,BP长为半径作弧,两弧相交于点Q;
(3)作直线PQ.
所以直线PQ就是所求的垂线.
请回答:该作图的依据是_________________________________________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AD⊥BC,EF垂直平分AC,交AC于点F,交BC于点E,且BD=DE.
⑴若∠BAE=40°,求∠C的度数;
⑵若△ABC周长13cm,AC=6cm,求DC长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一副三角板中的两块直角三角尺的直角顶点C按如图方式叠放在一起(其中,∠A=60°,∠D=30°;∠E=∠B=45°):
(1)①若∠DCE=45°,则∠ACB的度数为 ;
②若∠ACB=140°,求∠DCE的度数;
(2)由(1)猜想∠ACB与∠DCE的数量关系,并说明理由.
(3)当∠ACE<180°且点E在直线AC的上方时,这两块三角尺是否存在一组边互相平行?若存在,请直接写出∠ACE角度所有可能的值(不必说明理由);若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,D为BC边的中点,过点D作DE⊥AB,DF⊥AC,垂足分别为E,F.
(1)求证:△BED≌△CFD;
(2)若∠A=60°,BE=1,求△ABC的周长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com