【题目】如图，在ABCD中，AE⊥BD，CF⊥BD，E，F分别为垂足．
（1）求证：四边形AECF是平行四边形；
（2）如果AE=3，EF=4，求AF、EC所在直线的距离．
【答案】(1)证明见解析；(2) AF、EC所在直线的距离是2.4.
【解析】
(1) 先证△ADE≌△CBF，据此得出AD=BC，结合AD∥BC即可得证．
（2）根据勾股定理和三角形面积的不同计算方法即可解答.
(1)∵AE⊥BD，CF⊥BD，∴∠AED=∠CFB=90°，∴AE∥CF，在ABCD中，∵AD∥BC，∴∠ADE＝∠CBF，又∵AD＝CB，∴△ADE≌△CBF(AAS)，∴AE＝CF，∴四边形AECF是平行四边形(其他证法参照给分)；
(2)在AECF中，AF∥EC，设AF、EC所在直线的距离为h.∵AE⊥BD，∴∠AEF=90°，∴AF=
=5，∵SAECF=AE·EF=AF·h，∴h=
=2.4,∴AF、EC所在直线的距离是2.4.
字词句篇与同步作文达标系列答案科目：初中数学 来源： 题型：
【题目】定义：在同一平面内，如果矩形ABCD的四个顶点到⊙M上一点的距离相等，那么称这个矩形ABCD是⊙M的“伴侣矩形”．如图，在平面直角坐标系xOy中，直线l：y= 
x﹣3交x轴于点M，⊙M的半径为2，矩形ABCD沿直线运动（BD在直线l上），BD=2，AB∥y轴，当矩形ABCD是⊙M的“伴侣矩形”时，点C的坐标为（ ）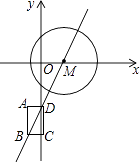
A.（ ﹣ 
，﹣ 
）
B.（ ﹣ 
，﹣ 
）
C.（ ﹣ ，﹣ ）或（ + ，﹣ ）
D.（ ﹣ ，﹣ ）或（ + ， ）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图,点P是正方形ABCD的对角线BD上一点,PE⊥BC于点E,PF⊥CD于点F,连接EF，给出下列五个结论:①AP=EF；②AP⊥EF；③△APD一定是等腰三角形；④∠PFE=∠BAP；⑤PD=
EC，其中正确结论的序号是______.
查看答案和解析>>
科目：初中数学 来源： 题型：
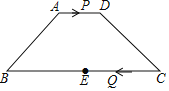
【题目】如图，在梯形ABCD中，
，
，
，E是BC的中点，点P以每秒1个单位长度的速度从点A出发，沿AD向点D运动；点Q同时以每秒2个单位长度的速度从点C出发，沿CB向点B运动
当点P停止运动时，点Q也随之停止运动当运动时间为______秒时，以点P、Q、E、D为顶点的四边形是平行四边形．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】小红同学在做作业时，遇到这样一道几何题：
已知：AB∥CD∥EF，∠A＝110°，∠ACE＝100°，过点E作EH⊥EF,垂足为E，交CD于H点．
（1）依据题意，补全图形；
（2）求∠CEH的度数．
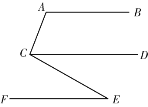
小明想了许久对于求∠CEH的度数没有思路，就去请教好朋友小丽，小丽给了他如图2所示的提示：
请问小丽的提示中理由①是 ；
提示中②是： 度；
提示中③是： 度；
提示中④是： ，理由⑤是 ．
提示中⑥是 度；
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在ABCD中，E是对角线BD上的一点，过点C作CF∥DB，且CF=DE，连接AE，BF，EF．
（1）求证：△ADE≌△BCF；
（2）若∠ABE+∠BFC=180°，则四边形ABFE是什么特殊四边形？说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】乘法公式的探究与应用：
（1）如图甲，边长为a的大正方形中有一个边长为b的小正方形，请你写出阴影部分的面积是
（2）小颗将阴影部分接下来，重新拼成一个长方形，如图乙，则长方形的长是 ，宽是 ，面积是 （写成多项式乘法的形式）．
（3）比较甲乙两图阴影部分的面积，可以得到恒等式
（4）运用你所得到的公式计算：10.3×9.7．
（5）若49x2﹣y2＝25，7x﹣y＝5，则7x+y的值为
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，四边形ABCD中，E、F、G、H依次是各边中点，O是四边形内一点，若S四边形AEOH=3，S四边形BFOE=4，S四边形CGOF=5，则S四边形DHOG= ． 
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，一段抛物线y=﹣x（x﹣3）（0≤x≤3），记为C1 ， 它与x轴交于点O，A1；将C1绕点A1旋转180°得C2 ， 交x 轴于点A2；将C2绕点A2旋转180°得C3 ， 交x 轴于点A3；…如此进行下去，得到一条“波浪线”．若点P（37，m）在此“波浪线”上，则m的值为 ．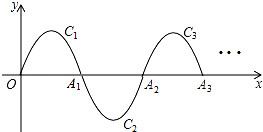 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com