
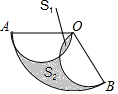
 如图,扇形OAB中,OA=OB=2,∠AOB=120°,分别以OA,OB为直径画半圆,若图中两个阴影部分面积分别记为S1与S2,则S2-S1的值是$\frac{1}{3}$π.
如图,扇形OAB中,OA=OB=2,∠AOB=120°,分别以OA,OB为直径画半圆,若图中两个阴影部分面积分别记为S1与S2,则S2-S1的值是$\frac{1}{3}$π. 分析 先求出扇形ABO的面积和两个半圆的面积,再根据S半圆AO+S半圆BO-S1+S2=S扇形ABO即可得S2-S1的值.
解答 解:扇形ABO的面积为$\frac{120•π•{2}^{2}}{360}$=$\frac{4}{3}$π,
两个半圆的面积均为$\frac{1}{2}$•π•12=$\frac{1}{2}$π,
∵S半圆AO+S半圆BO-S1+S2=S扇形ABO,
∴$\frac{1}{2}$π+$\frac{1}{2}$π+S2-S1=$\frac{4}{3}$π,
∴S2-S1=$\frac{4}{3}$π-π=$\frac{1}{3}$π,
故答案为:$\frac{1}{3}$π.
点评 本题主要考查扇形的面积计算,结合图形得出S半圆AO+S半圆BO-S1+S2=S扇形ABO是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
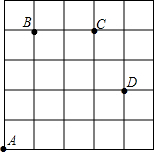 一只甲虫在5×5的方格(每小格边长为1m)上沿着网格线运动.它从A处出发去看望B、C、D处的其它甲虫(A,B,C,D都在格点上).规定:向上向右走为正,向下向左走为负.如果从A到B记为:A→B(+1,+4),从B到A记为:B→A(-1,-4),其中第一个数表示左右方向,第二个数表示上下方向,那么图中
一只甲虫在5×5的方格(每小格边长为1m)上沿着网格线运动.它从A处出发去看望B、C、D处的其它甲虫(A,B,C,D都在格点上).规定:向上向右走为正,向下向左走为负.如果从A到B记为:A→B(+1,+4),从B到A记为:B→A(-1,-4),其中第一个数表示左右方向,第二个数表示上下方向,那么图中查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 点P在⊙O上 | B. | 点P在⊙O外部 | C. | 点P在⊙O内部 | D. | 不能确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
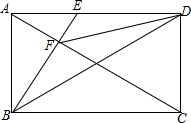 在矩形ABCD中,点E是AD的中点,BE垂直AC交AC于点F,求证:
在矩形ABCD中,点E是AD的中点,BE垂直AC交AC于点F,求证:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com