
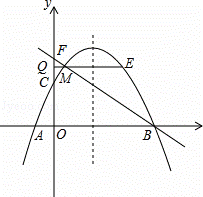
如图,抛物线y=ax2+bx+c(a≠0)与x轴交于A(﹣1,0),B(4,0)两点,与y轴交于点C(0,2),点M(m,n)是抛物线上一动点,位于对称轴的左侧,并且不在坐标轴上,过点M作x轴的平行线交y轴于点Q,交抛物线于另一点E,直线BM交y轴于点F.
(1)求抛物线的解析式,并写出其顶点坐标;
(2)当S△MFQ:S△MEB=1:3时,求点M的坐标.
解:(1)∵抛物线y=ax2+bx+c过点A(﹣1,0),B(4,0),C(0,2),
∴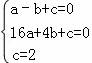 ,
,
解得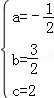 ,
,
∴y=﹣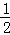 x2+
x2+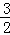 x+2,
x+2,
∵y=﹣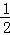 x2+
x2+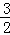 x+2=﹣
x+2=﹣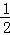 (x﹣3x+
(x﹣3x+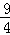 )+
)+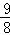 +2=﹣
+2=﹣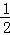 (x﹣
(x﹣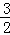 )2+
)2+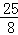 ,
,
∴顶点坐标为(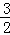 ,
,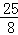 );
);
(2)∵M(m,n),
∴Q(0,n),E(3﹣m,n),
设直线BM的解析式为y=kx+b(k≠0),
把B(4,0),M(m,n)代入得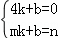 ,
,
解得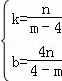 ,
,
∴y=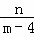 x+
x+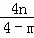 ,
,
令x=0,则y=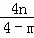 ,
,
∴点F的坐标为(0,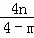 ),
),
∴MQ=|m|,FQ=|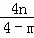 ﹣n|=|
﹣n|=|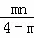 |,ME=|3﹣m﹣m|=|3﹣2m|,
|,ME=|3﹣m﹣m|=|3﹣2m|,
∴S△MFQ=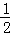 MQ•FQ=
MQ•FQ=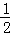 |m|•|
|m|•|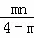 |=
|=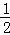 |
|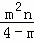 |,
|,
S△MEB=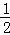 ME•|n|=
ME•|n|=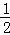 •|3﹣2m|•|n|,
•|3﹣2m|•|n|,
∵S△MFQ:S△MEB=1:3,
∴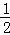 |
|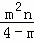 |×3=
|×3=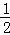 •|3﹣2m|•|n|,
•|3﹣2m|•|n|,
即|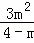 |=|3﹣2m|,
|=|3﹣2m|,
∵点M(m,n)在对称轴左侧,
∴m<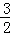 ,
,
∴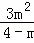 =3﹣2m,
=3﹣2m,
整理得,m2+11m﹣12=0,
解得m1=1,m2=﹣12,
当m1=1时,n1=﹣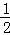 ×12+
×12+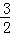 ×1+2=3,
×1+2=3,
当m2=﹣12时,n2=﹣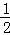 ×(﹣12)2+
×(﹣12)2+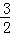 ×(﹣12)+2=﹣88,
×(﹣12)+2=﹣88,
∴点M的坐标为(1,3)或(﹣12,﹣88).


 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案科目:初中数学 来源: 题型:
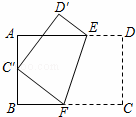
如图,将矩形ABCD沿EF折叠,使顶点C恰好落在AB边的中点C′上.若AB=6,BC=9,则BF的长为( )
|
| A. | 4 | B. | 3 | C. | 4.5 | D. | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:
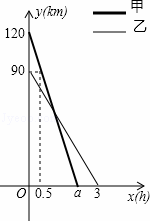
在一条笔直的公路旁依次有A、B、C三个村庄,甲、乙两人同时分别从A、B两村出发,甲骑摩托车,乙骑电动车沿公路匀速驶向C村,最终到达C村.设甲、乙两人到C村的距离y1,y2(km)与行驶时间x(h)之间的函数关系如图所示,请回答下列问题:
(1)A、C两村间的距离为 km,a= ;
(2)求出图中点P的坐标,并解释该点坐标所表示的实际意义;
(3)乙在行驶过程中,何时距甲10km?
查看答案和解析>>
科目:初中数学 来源: 题型:
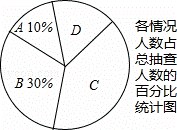
为了了解学生在一年中的课外阅读量,九(1)班对九年级800名学生采用随机抽样的方式进行了问卷调查,调查的结果分为四种情况:A.10本以下;B.10~15本;C.16~20本;D.20本以上.根据调查结果统计整理并制作了如图所示的两幅统计图表:
| 各种情况人数统计频数分布表 | ||||
| 课外阅读情况 | A | B | C | D |
| 频数 | 20 | x | y | 40 |
(1)在这次调查中一共抽查了 200 名学生;
(2)表中x,y的值分别为:x= 60 ,y= 80 ;
(3)在扇形统计图中,C部分所对应的扇形的圆心 角是 144 度;
角是 144 度;
(4)根据抽样调查结果,请估计九年级学生一年阅读课外书20本以上的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
如表是10支不同型号签字笔的相关信息,则这10支签字笔的平均价格是( )
| 型号 | A | B | C |
| 价格(元/支) | 1 | 1.5 | 2 |
| 数量(支) | 3 | 2 | 5 |
|
| A. | 1.4元 | B. | 1.5元 | C. | 1.6元 | D. | 1.7元 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com