
分析 根据题意可求得a=-1,b=2,然后将a、b的值代入,最后利用拆项裂项法求解即可.
解答 解:∵|a+1|与(b-2)2互为相反数,
∴|a+1|+(b-2)2=0.
∴a=-1,b=2.
∴原式=$\frac{1}{1×2}$+$\frac{1}{2×3}$+$\frac{1}{3×4}$+…+$\frac{1}{2011×2012}$
=$1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}$+…+$\frac{1}{2011}-\frac{1}{2012}$
=1-$\frac{1}{2012}$
=$\frac{2011}{2012}$.
点评 本题主要考查的是求代数式的值,拆项裂项法的应用是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 分组 | 频数累计 | 频数 | 频率 |
| 0.55~1.05 | 正正 | 14 | 0.28 |
| 1.05~1.55 | 正正正 | 15 | 0.30 |
| 1.55~2.05 | 正 | 7 | 0.14 |
| 2.05~2.55 |  | 4 | 0.08 |
| 2.55~3.05 | 正 | 5 | 0.10 |
| 3.05~3.55 | 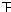 | 3 | 0.06 |
| 3.55~4.05 | 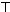 | 2 | 0.04 |
| 合计 | 50 | 1.00 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
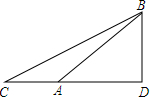 某商场准备改善原有楼梯的安全性能,把倾斜角由原来的40°减至35°.已知原楼梯AB的长为5m,调整后的楼梯所占地面CD有多长?(结果精确到0.1m)
某商场准备改善原有楼梯的安全性能,把倾斜角由原来的40°减至35°.已知原楼梯AB的长为5m,调整后的楼梯所占地面CD有多长?(结果精确到0.1m)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com