Question

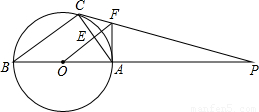
如图，△ABC内接与⊙O，AB是直径，⊙O的切线PC交BA的延长线于点P，OF∥BC交AC于AC点E，交PC于点F，连接AF．

（1）判断AF与⊙O的位置关系并说明理由；

（2）若⊙O的半径为4，AF=3，求AC的长．

 

Answer 1

【答案】

（1）详见试题解析; （2）

【解析】

试题分析：（1）AF为为圆O的切线，理由为：练级OC，由PC为圆O的切线，利用切线的性质得到CP垂直于OC，由OF与BC平行，利用两直线平行内错角相等，同位角相等，分别得到两对角相等，根据OB=OC，利用等边对等角得到一对角相等，等量代换得到一对角相等，再由OC=OA，OF为公共边，利用SAS得出三角形AOF与三角形COF全等，由全等三角形的对应角相等及垂直定义得到AF垂直于OA，即可得证；

（2）由AF垂直于OA，在直角三角形AOF中，由OA与AF的长，利用勾股定理求出OF的长，而OA=OC，OF为角平分线，利用三线合一得到E为AC中点，OE垂直于AC，利用面积法求出AE的长，即可确定出AC的长．

试题解析：（1）AF为圆O的切线，理由为：

连接OC，

∵PC为圆O切线，

∴CP⊥OC，

∴∠OCP=90°，

∵OF∥BC，

∴∠AOF=∠B，∠COF=∠OCB，

∵OC=OB，

∴∠OCB=∠B，

∴∠AOF=∠COF，

∵在△AOF和△COF中，

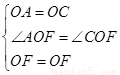
∴△AOF≌△COF（SAS），

∴∠OAF=∠OCF=90°，

则AF为圆O的切线；

（2）∵△AOF≌△COF，

∴∠AOF=∠COF，

∵OA=OC，

∴E为AC中点，即AE=CE=AC，OE⊥AC，

∵OA⊥AF，

∴在Rt△AOF中，OA=4，AF=3，

根据勾股定理得：OF=5，

∵S_△AOF=OA•AF=•OF•AE，

∴AE=，

则AC=2AE=．

考点： 切线的判定与性质．