
【题目】如图,矩形OABC的顶点A、C分别在x轴、y轴上,OA=4,OC=3,直线m:y=﹣![]() x从原点O出发,沿x轴正方向以每秒1个单位长度的速度运动,设直线m与矩形OABC的两边分别交于点M,N,直线m运动的时间为t(秒),设△OMN的面积为S,则能反映S与t之间函数关系的大致图象是( )
x从原点O出发,沿x轴正方向以每秒1个单位长度的速度运动,设直线m与矩形OABC的两边分别交于点M,N,直线m运动的时间为t(秒),设△OMN的面积为S,则能反映S与t之间函数关系的大致图象是( )

A. 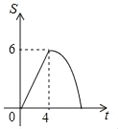 B.
B. 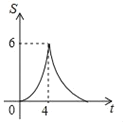 C.
C. 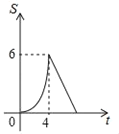 D.
D. 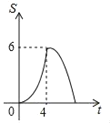
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:
【题目】 已知抛物线y=![]() x2+bx+c经过点A(-2,0),B(0,-4)与x轴交于另一点C,连接BC.
x2+bx+c经过点A(-2,0),B(0,-4)与x轴交于另一点C,连接BC.

(1)求抛物线的解析式;
(2)如图,P是第一象限内抛物线上一点,BP交x轴于点E,且S△PBO=S△PBC,求证:E是OC的中点;
(3)在(2)的条件下求点P的坐标.
(4)在(2)的条件下拋物线上是否存在点D,使△ACD的面积与△ABP的面积相等?若存在,请求出点D的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0)与x轴交于A、B两点,与y轴交于点C(0,3),且OB=OC=3AO.直线y=x+1与抛物线交于A、D两点,与y轴交于点E,点Q是抛物线的顶点,设直线AD上方的抛物线上的动点P的横坐标为m.
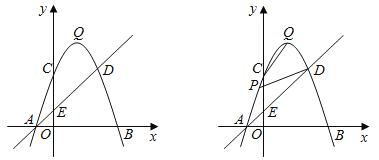
(1)求该抛物线的解析式及顶点Q的坐标;
(2)连结CQ,判断线段CQ与线段AE的数量关系和位置关系,并说明理由.
(3)连结PA、PD,当m为何值时,S△PAD=![]() S△DAB;
S△DAB;
(4)在直线AD上是否存在一点H使△PQH为等腰直角三角形,若存在请求出m的值,不存在请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
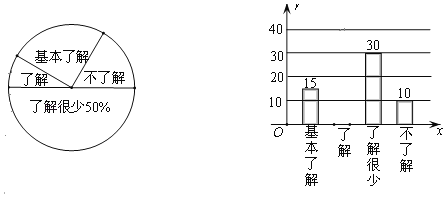
【题目】“食品安全”受到全社会的广泛关注,武汉市某中学对部分学生就食品安全知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了下面两幅尚不完整的统计图.请你根据统计图中所提供的信息解答下列问题:
(1)接受问卷调查的学生共有 人,扇形统计图中“了解”部分所对应扇形的圆心角为 ;
(2)若从对食品安全知识达到“了解”程度的2个女生和2个男生中随机抽取2人参加食品安全知识竞赛,恰好抽到1个男生和1个女生的概率为 ;
(3)若该中学共有学生900人,请根据上述调查结果,估计该中学学生中对食品安全知识达到“了解”和“基本了解”程度的总人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若关于x的一元二次方程(m+1)x2﹣2x﹣1=0有两个不相等的实数根,
(1)求m的取值范围;
(2)若x=1是方程的一个根,求m的值和另一个根.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】老师留在小黑板上的题如图所示.小彬说:该抛物线过点![]() ;小明说:
;小明说:![]() ;小颖说:该抛物线在
;小颖说:该抛物线在![]() 轴上截得的线段长为
轴上截得的线段长为![]() .你认为三人的说法中,正确的有( )
.你认为三人的说法中,正确的有( )

A.![]() 个B.
个B.![]() 个C.
个C.![]() 个D.
个D.![]() 个
个
查看答案和解析>>
科目:初中数学 来源: 题型:
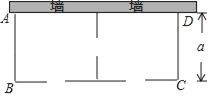
【题目】某农场要建一个饲养场(长方形ABCD),饲养场的一面靠墙(墙最大可用长度为27米),另三边用木栏围成,中间也用木栏隔开,分成两个场地,并在如图所示的三处各留1米宽的门(不用木栏),建成后木栏总长57米,设饲养场(长方形ABCD)的宽为a米.
(1)饲养场的长为多少米(用含a的代数式表示).
(2)若饲养场的面积为288m2,求a的值.
(3)当a为何值时,饲养场的面积最大,此时饲养场达到的最大面积为多少平方米?
查看答案和解析>>
科目:初中数学 来源: 题型:
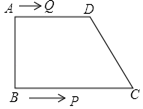
【题目】如图,在四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,点
,点![]() 从点
从点![]() 出发以
出发以![]() 的速度向点
的速度向点![]() 运动,点
运动,点![]() 从点
从点![]() 出发以
出发以![]() 的速度向
的速度向![]() 点运动,
点运动,![]() 、
、![]() 两点同时出发,其中一点到达终点时另一点也停止运动.若
两点同时出发,其中一点到达终点时另一点也停止运动.若![]() ,当
,当![]() __
__![]() 时,
时,![]() 是等腰三角形.
是等腰三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的图象如图所示,下列结论:①ac<0,②b﹣2a<0,③b2﹣4ac<0,④a﹣b+c<0,正确的是( )
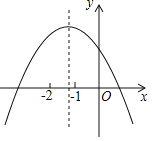
A.①②B.①④C.②③D.②④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com