
分析 (1)①根据新定义直接判断,②由A1B1∥AB得到$\frac{OA}{O{A}_{1}}=\frac{AB}{{A}_{1}{B}_{1}}=\frac{2}{4}=\frac{1}{2}$,求出即可;
(2)分两种情况计算①当⊙E与y轴相切时,②当⊙E与直线OI相切时,求出角,线段用锐角三角函数求解即可;
(3)先判断出只有当N'TQN''共线时,l取得最小值N'N'',Q,T的位置,用△OGM∽△OHQ,得出比例式计算出HQ,最后用勾股定理求解即可.
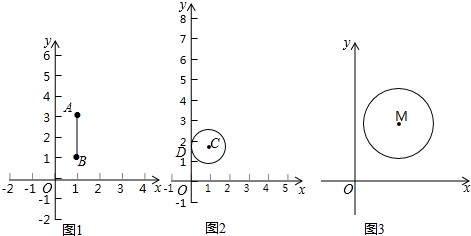
解答 解(1)①线段OP与图形W无公共点,则称点P为关于图形W的“阳光点”,
∴OP1与线段AB没有公共点,OP2与线段AB有公共点(1,2),OP3与线段AB有公共点(1,$\frac{3}{2}$),OP4与线段AB没公共点,
∴关于线段AB的“阳光点”是P1,P4,
故答案为P1,P4
②∵A1B1∥AB,
∴$\frac{OA}{O{A}_{1}}=\frac{AB}{{A}_{1}{B}_{1}}=\frac{2}{4}=\frac{1}{2}$,
∵点A1在B1的上方
∴A1(2,6),
故答案为(2,6),
(2)情况一:
当⊙E与y轴相切时,设切点为F,连接EF
∵⊙E与y轴相切于点F,
∴EF⊥y轴
∵⊙E的半径为$\frac{3}{2}$
∴EF=$\frac{3}{2}$
∴此时点E的横坐标为$\frac{3}{2}$
情况二:
设直线l分别与x轴,y轴交于点G,H,连接CD,CO,过点O作⊙C的另一条切线OI,切点为I,直线OI与直线l交于点J,
当⊙E与直线OI相切时,过点E作EK⊥y轴于点K
∵⊙C与y轴相切于点D,
∴CD⊥y轴
∵点C的坐标(1,$\sqrt{3}$)
∴tan∠COD=$\frac{\sqrt{3}}{3}$
∴∠COD=30°,
∵⊙C与OI相切于点I
∴∠COI=∠COD=30°
∴∠HOJ=∠COI+∠COD=90°
∵直线l:y=-$\sqrt{3}$x+4$\sqrt{3}$分别与x轴,y轴交于点G,H,
∴点 G(4,0),H(0,4$\sqrt{3}$)
∴tan∠OHG=$\frac{\sqrt{3}}{3}$
∴∠OHG=30°
∴∠OJH=180°-∠HOJ-∠OHJ=90°
∴HG⊥OJ
∵⊙E与直线OJ相切,
∴切点为点J
∴EJ=$\frac{3}{2}$
∵在Rt△OHJ中,HJ=OH×cos∠OHJ=6
∴HE=HJ-EJ=$\frac{9}{2}$
∴KH=$\frac{1}{2}$HE=$\frac{9}{4}$
∴此时点E的横坐标为$\frac{9}{4}$
可知,点E在直线l上,从情况一中的位置运动到情况二中的位置时,都满足题意,所以点E的横坐标的取值范围 $\frac{3}{2}$≤xE≤$\frac{9}{4}$
(3)如图: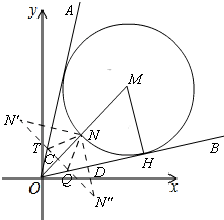
连接OM,交圆于N,OA与OB分别于⊙M相切,
则N点在OA与OB上对称点分别为N'与N'';连接N'N''交OA于T,交OB于Q,交OM于C,
△NTQ的周长l=TN+TQ+QN=TN'+TQ+QN'';
只有当N'、T、Q、N''共线时,l取得最小值N'N'',
此时的T与Q即为所求;
由辅助线知,∠MHO=∠NDO=90°,NN″=2CN″,
sin∠MOH=$\frac{MH}{OM}$=$\frac{DN}{ON}$=$\frac{3}{5}$,
∴$\frac{3}{5}$=$\frac{DN}{2}$,
∴DN=$\frac{6}{5}$,
∴NN″=2DN=$\frac{12}{5}$,
∵∠N''+∠DQN''=90°,
∠CQO+∠COQ=90°,
∴∠N″=∠MOH,
∴sin∠N″=$\frac{3}{5}$,
∴cos∠N″=$\frac{4}{5}$=$\frac{CN″}{NN″}$,
∴CN″=$\frac{48}{25}$,
∴N'N″=2CN″=$\frac{96}{25}$,
∴△NQT的周长最小值l=N'N″=$\frac{96}{25}$.
点评 此题是圆的综合题,主要考查了新定义的理解,相似三角形的性质和判定,圆的切线的性质,解本题的关键是理解新定义,难点是确定△NTQ周长最小时的点Q,T的位置.


科目:初中数学 来源: 题型:解答题
 某工厂要制作一个容积为300立方厘米的正方体形状的无盖水槽(如图所示).准备用钢板焊制,试求至少要用多少平方厘米的钢板?(结果精确到1平方厘米)
某工厂要制作一个容积为300立方厘米的正方体形状的无盖水槽(如图所示).准备用钢板焊制,试求至少要用多少平方厘米的钢板?(结果精确到1平方厘米)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $-\frac{1}{3}<-\frac{3}{2}<-0.2<-1$ | B. | $-\frac{1}{3}<-0.2<-1<-\frac{3}{2}$ | C. | $-\frac{3}{2}>-1>-\frac{1}{3}>-0.2$ | D. | $-0.2>-\frac{1}{3}>-1>-\frac{3}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
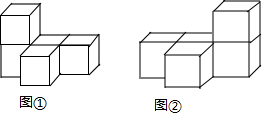
| A. | 主视图 | B. | 俯视图 | ||
| C. | 左视图 | D. | 主视图、俯视图和左视图都不同 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
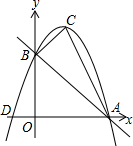 如图,已知直线y=-x+3的图象分别交x轴于A点,交y轴于B点,抛物线y=-x2+bx+c经过点A、B两点,并与x轴交于另一点D,顶点为C.
如图,已知直线y=-x+3的图象分别交x轴于A点,交y轴于B点,抛物线y=-x2+bx+c经过点A、B两点,并与x轴交于另一点D,顶点为C.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0.286×105 | B. | 2.86×104 | C. | 2.86×105 | D. | 28.6×103 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com