
【题目】如图,在四边形ABCD中,AB=AD=6,AB⊥BC,AD⊥CD,∠BAD=60°,点M、N分别在AB、AD边上,若AM:MB=AN:ND=1:2,则tan∠MCN=

【答案】![]()
【解析】试题分析:连接AC,通过三角形全等,求得∠BAC=30°,从而求得BC的长,然后根据勾股定理求得CM的长,连接MN,过M点作ME⊥CN于E,则△MNA是等边三角形求得MN=2,设NE=x,表示出CE,根据勾股定理即可求得ME,然后求得tan∠MCN.
试题解析:∵AB=AD=6,AM:MB=AN:ND=1:2,
∴AM=AN=2,BM=DN=4,
连接MN,连接AC,

∵AB⊥BC,AD⊥CD,∠BAD=60°
在Rt△ABC与Rt△ADC中,
![]() ,
,
∴Rt△ABC≌Rt△ADC(HL)
∴∠BAC=∠DAC=![]() ∠BAD=30°,MC=NC,
∠BAD=30°,MC=NC,
∴BC=![]() AC,
AC,
∴AC2=BC2+AB2,即(2BC)2=BC2+AB2,
3BC2=AB2,
∴BC=2![]() ,
,
在Rt△BMC中,CM=![]()
∵AN=AM,∠MAN=60°,
∴△MAN是等边三角形,
∴MN=AM=AN=2,
过M点作ME⊥CN于E,设NE=x,则CE=2![]() -x,
-x,
∴MN2-NE2=MC2-EC2,即4-x2=(2![]() )2-(2
)2-(2![]() -x)2,
-x)2,
解得:x=![]() ,
,
∴EC=2![]() -
-![]() =
=![]() ,
,
∴ME=![]() ,
,
∴tan∠MCN=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图1,在△ABC中,∠BAC=90°,AB=AC,在△ABC内部作△CED,使∠CED=90°,E在BC上,D在AC上,分别以AB,AD为邻边作平行四边形ABFD,连接AF、AE、EF.
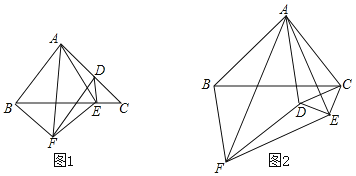
(1)证明:AE=EF;
(2)判断线段AF,AE的数量关系,并证明你的结论;
(3)在图(1)的基础上,将△CED绕点C逆时针旋转,请判断(2)问中的结论是否成立?若成立,结合图(2)写出证明过程;若不成立,请说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“一带一路”国际合作高峰论坛期间,我国同30多个国家签署经贸合作协议.某工厂准备生产甲、乙两种商品共6万件销往“一带一路”沿线国家和地区,已知2件甲种商品与3件乙种商品的销售收入相同,3件甲种商品比2件乙种商品的销售收入多1500元.
(1)甲种商品与乙种商品的销售单价各多少元?
(2)若甲、乙两种商品的销售总收入不低于4200万元,则至少销管甲种商品多少万件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)5![]() ﹣(﹣2
﹣(﹣2![]() )+(﹣3
)+(﹣3![]() )﹣(+4
)﹣(+4![]() )
)
(2)(﹣![]() ﹣
﹣![]() +
+![]() )×(﹣24)
)×(﹣24)
(3)(﹣3)÷![]() ×
×![]() ×(﹣15)
×(﹣15)
(4)﹣14+|(﹣2)3﹣10|﹣(﹣3)÷(﹣1)2017.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市提倡“诵读中华经典,营造书香校园”的良好诵读氛围,促进校园文化建设,进而培养学生的良好诵读习惯,使经典之风浸漫校园.某中学为了了解学生每周在校经典诵读时间,在本校随机抽取了若干名学生进行调查,并依据调查结果绘制了以下不完整的统计图表,请根据图表信息解答下列问题:
时间(小时) | 频数(人数) | 频率 |
2≤t<3 | 4 | 0.1 |
3≤t<4 | 10 | 0.25 |
4≤t<5 | a | 0.15 |
5≤t<6 | 8 | b |
6≤t<7 | 12 | 0.3 |
合计 | 40 | 1 |
(1)表中的a= ,b= ;
(2)请将频数分布直方图补全;
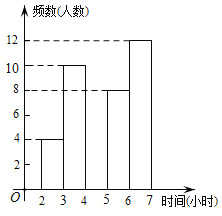
(3)若该校共有1200名学生,试估计全校每周在校参加经典诵读时间至少有4小时的学生约为多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx经过点A(﹣1,![]() )及原点,交x轴于另一点C(2,0),点D(0,m)是y轴正半轴上一动点,直线AD交抛物线于另一点B.
)及原点,交x轴于另一点C(2,0),点D(0,m)是y轴正半轴上一动点,直线AD交抛物线于另一点B.
(1)求抛物线的解析式;
(2)如图1,连接AO、BO,若△OAB的面积为5,求m的值;
(3)如图2,作BE⊥x轴于E,连接AC、DE,当D点运动变化时,AC、DE的位置关系是否变化?请证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某智能手机越来越受到大众的喜爱,各种款式相继投放市场,某店经营的A款手机去年销售总额为50000元,今年每部销售价比去年降低400元,若卖出的数量相同,销售总额将比去年减少20%.
已知A,B两款手机的进货和销售价格如下表:
A款手机 | B款手机 | |
进货价格(元) | 1100 | 1400 |
销售价格(元) | 今年的销售价格 | 2000 |
(1)今年A款手机每部售价多少元?
(2)该店计划新进一批A款手机和B款手机共90部,且B款手机的进货数量不超过A款手机数量的两倍,应如何进货才能使这批手机获利最多?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在平面直角坐标系![]() 中,直线
中,直线![]() 分别交
分别交![]() 、
、![]() 轴于点A、B两点,OA=5,∠OAB=60°.
轴于点A、B两点,OA=5,∠OAB=60°.
(1)如图1,求直线AB的解析式;
(2)如图2,点P为直线AB上一点,连接OP,点D在OA延长线上,分别过点P、D作OA、OP的平行线,两平行线交于点C,连接AC,设AD=m,△ABC的面积为S,求S与m的函数关系式;
(3)如图3,在(2)的条件下,在PA上取点E ,使PE=AD, 连接EC,DE,若∠ECD=60°,四边形ADCE的周长等于22,求S的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com