
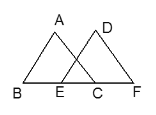
【题目】如图,已知AB∥DE,AB=DE,请你添加一个条件_______ 可以根据“ASA”使得△ABC≌△DEF;或者添加条件BE=CF,可以根据_______得到△ABC≌△DEF。
科目:初中数学 来源: 题型:
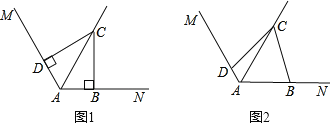
【题目】已知∠MAN=120°,AC平分∠MAN,点B、D分别在AN、AM上.
(1)如图1,若∠ABC=∠ADC=90°,请你探索线段AD、AB、AC之间的数量关系,并证明之;
(2)如图2,若∠ABC+∠ADC=180°,则(1)中的结论是否仍然成立?若成立,给出证明;若不成立,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
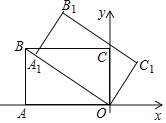
【题目】如图,平面直角坐标系中,矩形OABC的顶点A(﹣6,0),C(0,2![]() ).将矩形OABC绕点O顺时针方向旋转,使点A恰好落在OB上的点A1处,则点B的对应点B1的坐标为_____.
).将矩形OABC绕点O顺时针方向旋转,使点A恰好落在OB上的点A1处,则点B的对应点B1的坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
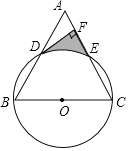
【题目】已知:如图,以等边△ABC的边BC为直径作⊙O,分别交AB,AC于点D,E,过点D作DF⊥AC交AC于点F.
(1)求证:DF是⊙O的切线;
(2)若等边△ABC的边长为8,求由![]() 、DF、EF围成的阴影部分面积.
、DF、EF围成的阴影部分面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
已知:如图1,等边△A1A2A3内接于⊙O,点P是![]() 上的任意一点,连接PA1,PA2,PA3,可证:PA1+PA2=PA3,从而得到:
上的任意一点,连接PA1,PA2,PA3,可证:PA1+PA2=PA3,从而得到:![]() 是定值.
是定值.
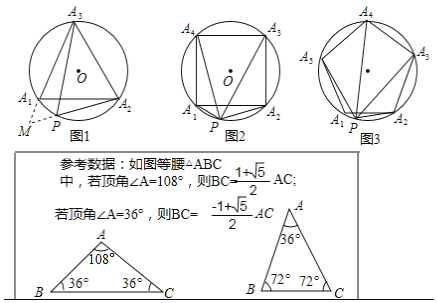
(1)以下是小红的一种证明方法,请在方框内将证明过程补充完整;
证明:如图1,作∠PA1M=60°,A1M交A2P的延长线于点M.
∵△A1A2A3是等边三角形,
∴∠A3A1A2=60°,
∴∠A3A1P=∠A2A1M
又A3A1=A2A1,∠A1A3P=∠A1A2P,
∴△A1A3P≌△A1A2M

∴PA3=MA2=PA2+PM=PA2+PA1.
∴![]() ,是定值.
,是定值.
(2)延伸:如图2,把(1)中条件“等边△A1A2A3”改为“正方形A1A2A3A4”,其余条件不变,请问:![]() 还是定值吗?为什么?
还是定值吗?为什么?
(3)拓展:如图3,把(1)中条件“等边△A1A2A3”改为“正五边形A1A2A3A4A5”,其余条件不变,则![]() = (只写出结果).
= (只写出结果).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,C,D为线段AB上的两点,M,N分别是线段AC,BD的中点.
(1)如果CD=5cm,MN=8cm,求AB的长;
(2)如果AB=a,MN=b,求CD的长.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, BD 是△ABC 的角平分线, AE⊥ BD ,垂足为 F ,若∠ABC=35°,∠ C=50°,则∠CDE 的度数为( )

A.35°B.40°C.45°D.50°
查看答案和解析>>
科目:初中数学 来源: 题型:
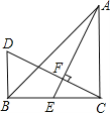
【题目】如图,△ABC中,∠ACB=90°,AC=BC,E是BC边上的一点,连接AE,过C作CF⊥AE,垂足为F,过B作BD⊥BC交CF的延长线于D.
(1)求证:△ACE≌△CBD;
(2)若BE=3![]() ,AB=6
,AB=6![]() ,求点E到AB的距离.
,求点E到AB的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com