
 ��ͼ����֪Rt��ABC�У���C=90�㣬AC=8��BC=6����P��ÿ��1����λ���ٶȴ�A��C�˶���ͬʱ��Q��ÿ��2����λ���ٶȴ�A��B��C�����˶������ǵ�C���ֹͣ�˶������P��Q�˶���ʱ��Ϊt�룮
��ͼ����֪Rt��ABC�У���C=90�㣬AC=8��BC=6����P��ÿ��1����λ���ٶȴ�A��C�˶���ͬʱ��Q��ÿ��2����λ���ٶȴ�A��B��C�����˶������ǵ�C���ֹͣ�˶������P��Q�˶���ʱ��Ϊt�룮���� ��1����ͼ1����Q��QE��AC��E������PQ���ɡ�ABC�ס�AQE���õ�����ʽ$\frac{AQ}{AB}=\frac{AE}{AC}=\frac{QE}{BC}$�����PE=$\frac{3}{5}t$��QE=$\frac{6}{5}t$�����ݹ��ɶ����õ�PQ2=QE2+PE2�����PQ=$\frac{3\sqrt{5}}{5}$t����Q��B�غ�ʱ��PQ��ֵ������ǵõ���t=5ʱ��PQ�����ֵ=3$\sqrt{5}$��
��2���������ε������ʽ������ã�
��3�����ڣ���ͼ2������CQ��PQ������������ٵ�CQ=CPʱ���ڵ�PQ=CQʱ���۵�PQ=PCʱ���з�����⼴�ɣ�
��� �⣺��1����ͼ1����Q��QE��AC��E������PQ��
�ߡ�C=90�㣬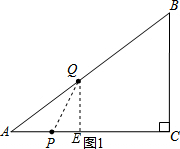
��QE��BC��
���ABC�ס�AQE��
��$\frac{AQ}{AB}=\frac{AE}{AC}=\frac{QE}{BC}$��
��AQ=2t��AP=t��
�ߡ�C=90�㣬AC=8��BC=6��
��AB=10��
��$\frac{2t}{10}=\frac{t+PE}{8}=\frac{QE}{6}$��
��PE=$\frac{3}{5}t$��QE=$\frac{6}{5}t$��
��PQ2=QE2+PE2��
��PQ=$\frac{3\sqrt{5}}{5}$t��
��Q��B�غ�ʱ��PQ��ֵ���
�൱t=5ʱ��PQ�����ֵ=3$\sqrt{5}$��
��2����ͼ1����ABC��ֱ��PQɨ�������=S��AQP��
��Q��AB����ʱ��S=$\frac{1}{2}$AP•QE=$\frac{1}{2}$t•$\frac{6}{5}t$=${\frac{3}{5}t}^{2}$����0��t��5��
��Q��BC����ʱ����ABC��ֱ��PQɨ�������=S�ı���ABQP��
��S�ı���ABQP=S��ABC-S��PQC=$\frac{1}{2}$��8��6-$\frac{1}{2}$��8-t��•��16-2t��=-t2+16t-40����5��t��8����
�ྭ��t����˶�����ABC��ֱ��PQɨ�������S��ʱ��t�ĺ�����ϵʽ�ǣ�
S=$\left\{\begin{array}{l}{\frac{3}{5}{t}^{2}��0��t��5��}\\{-{t}^{2}+16t-40��5��t��8��}\end{array}\right.$��
��3�����ڣ�
����Q��AB����ʱ����ͼ2������CQ��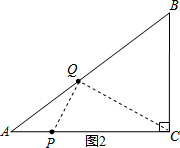 PQ��
PQ��
�ɣ�1��֪QE=$\frac{6}{5}t$��CE=AC-AE=8-$\frac{8}{5}t$��PQ=$\frac{3\sqrt{5}}{5}$t��
��CQ=$\sqrt{{QE}^{2}{+CE}^{2}}$=$\sqrt{{��\frac{6}{5}t��}^{2}{+��8-\frac{8}{5}t��}^{2}}$=$\sqrt{{4t}^{2}-\frac{128}{5}t+64}$=2$\sqrt{{t}^{2}-\frac{32}{5}t+16}$��
�ٵ�CQ=CPʱ��
����2$\sqrt{{t}^{2}-\frac{32}{5}t+16}$=8-t��
��ã�t=$\frac{16}{5}$��
�ڵ�PQ=CQʱ��
����$\frac{3\sqrt{5}}{5}$t=2$\sqrt{{t}^{2}-\frac{32}{5}t+16}$��
��ã�t=$\frac{40}{11}$��t=8������������ȥ����
�۵�PQ=PCʱ��
��$\frac{3\sqrt{5}}{5}$t=8-t��
��ã�t��3.4��
����Q��BC����ʱ��
�ߡ�ACB=90�㣬
���PQC�ǵ���ֱ�������Σ�
��CQ=CP��
��8-t=16-2t��
��t=8����P��Q��C�غϣ��������⣬
������������t=$\frac{16}{5}$��t=$\frac{40}{11}$��t=3.4ʱ����PQCΪ���������Σ�
���� ���⿼���˶������⣬���������ε��ж������ʣ������ε���������ɶ��������������ε����ʣ��ر��ǣ�3��Ҫ�������ۣ���Ҫ©�⣮


 Ӧ������ҵ��ϵ�д�
Ӧ������ҵ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | x=2 | B�� | x��2 | C�� | x=-2 | D�� | x��-2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
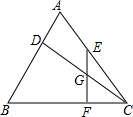 ��֪��AB=AC��EF��BC��F��CD��AB��EG=CF����$\frac{AD}{BD}$��ֵ��
��֪��AB=AC��EF��BC��F��CD��AB��EG=CF����$\frac{AD}{BD}$��ֵ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | x��2 | B�� | x��2��x��1 | C�� | x��2��x��1 | D�� | x��1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����һ������洹ֱ��Χǽ��ͬ����һ����10�����AB��һ���߶�δ֪�ĵ��߸�CD�����Ƕ�����洹ֱ��Ϊ�˲�õ��߸˵ĸ߶ȣ�һ��С���ͬѧ���������²�����ijһʱ�̣���̫���������£��������Χǽ�ϵ�Ӱ��EF�ij���Ϊ2�ף����ڵ����ϵ�Ӱ��BF�ij�Ϊ10�ף������߸�����Χǽ�ϵ�Ӱ��GH�ij���Ϊ3�ף����ڵ����ϵ�Ӱ��DH�ij�Ϊ5�ף�������Щ���ݣ���С���ͬѧ������˵��߸˵ĸ߶ȣ�
��ͼ����һ������洹ֱ��Χǽ��ͬ����һ����10�����AB��һ���߶�δ֪�ĵ��߸�CD�����Ƕ�����洹ֱ��Ϊ�˲�õ��߸˵ĸ߶ȣ�һ��С���ͬѧ���������²�����ijһʱ�̣���̫���������£��������Χǽ�ϵ�Ӱ��EF�ij���Ϊ2�ף����ڵ����ϵ�Ӱ��BF�ij�Ϊ10�ף������߸�����Χǽ�ϵ�Ӱ��GH�ij���Ϊ3�ף����ڵ����ϵ�Ӱ��DH�ij�Ϊ5�ף�������Щ���ݣ���С���ͬѧ������˵��߸˵ĸ߶ȣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��֪���κ���y=ax2+bx+c+2��ͼ����ͼ��ʾ������Ϊ��-1��0�������н��ۣ���abc��0����b2-4ac=0����a��2����4a-2b+c��0��������ȷ���۵ĸ����ǣ�������
��֪���κ���y=ax2+bx+c+2��ͼ����ͼ��ʾ������Ϊ��-1��0�������н��ۣ���abc��0����b2-4ac=0����a��2����4a-2b+c��0��������ȷ���۵ĸ����ǣ�������| A�� | 1 | B�� | 2 | C�� | 3 | D�� | 4 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com