
 如图,菱形ABCD的对角线AC=3cm,把它沿对角线AC方向平移1cm得到菱形EFGH,则图中阴影部分图形的面积与四边形ENCM的面积之比为( )
如图,菱形ABCD的对角线AC=3cm,把它沿对角线AC方向平移1cm得到菱形EFGH,则图中阴影部分图形的面积与四边形ENCM的面积之比为( )| A. | 9:4 | B. | 12:5 | C. | 3:1 | D. | 5:2 |
分析 首先得出△MEC∽△DAC,则 $\frac{EC}{AC}$=$\frac{ME}{AD}$,进而得出 $\frac{{S}_{△CME}}{{S}_{△ADC}}$=$\frac{4}{9}$,即可得出答案.
解答 解:∵ME∥AD,
∴△MEC∽△DAC,
∴$\frac{EC}{AC}$=$\frac{ME}{AD}$,
∵菱形ABCD的对角线AC=3cm,把它沿着对角线AC方向平移1cm得到菱形EFGH,
∴AE=1cm,EC=2cm,
∴$\frac{EC}{AC}$=$\frac{2}{3}$,
∴$\frac{{S}_{△CME}}{{S}_{△ADC}}$=$\frac{4}{9}$,
∴图中阴影部分图形的面积与四边形EMCN的面积之比为:$\frac{5+5+5+5}{4+4}$=$\frac{5}{2}$.
故选D.
点评 此题主要考查了菱形的性质以及相似三角形的判定与性质,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.


 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案科目:初中数学 来源: 题型:选择题
| A. | 30 cm2 | B. | 15 cm2 | C. | 30π cm2 | D. | 15π cm2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2x2+3x2=5x4 | B. | 2x2-3x2=-1 | C. | 2x2÷3x2=$\frac{2}{3}$x2 | D. | 2x2•3x2=6x4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
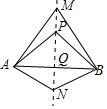 如图,直线MN是四边形AMBN的对称轴,与对角线交与点Q,点P是直线MN上面一点,下列判断错误的是( )
如图,直线MN是四边形AMBN的对称轴,与对角线交与点Q,点P是直线MN上面一点,下列判断错误的是( )| A. | AQ=BQ | B. | AP=BP | C. | ∠MAP=∠MBP | D. | ∠ANM=∠NMB |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
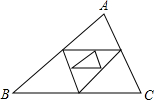 如下图,已知△ABC周长为1,连结△ABC三边的中点构成第二个三角形,再连结第二个三角形三边中点构成第三个三角形,依此类推,第2017个三角形周长为( )
如下图,已知△ABC周长为1,连结△ABC三边的中点构成第二个三角形,再连结第二个三角形三边中点构成第三个三角形,依此类推,第2017个三角形周长为( )| A. | $\frac{1}{2016}$ | B. | $\frac{1}{2017}$ | C. | $\frac{1}{{2}^{2016}}$ | D. | $\frac{1}{{2}^{2017}}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com